
ЁОЬтФПЁПЃЈБОЬтТњЗж![]() ЗжЃЉ
ЗжЃЉ
ЃЈ![]() ЃЉЁОЮЪЬтЁПШчЭМ
ЃЉЁОЮЪЬтЁПШчЭМ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЭтвЛЖЏЕуЃЌЧв
ЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЎЕБЕу
ЃЎЕБЕу![]() ЮЛгк__________ЪБЯпЖЮ
ЮЛгк__________ЪБЯпЖЮ![]() ЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊ__________ЃЈгУКЌ
ЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊ__________ЃЈгУКЌ![]() ЁЂ
ЁЂ![]() ЕФЪНзгБэЪОЃЉЃЎ
ЕФЪНзгБэЪОЃЉЃЎ
ЃЈ![]() ЃЉЁОгІгУЁПЕу
ЃЉЁОгІгУЁПЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() Г§ЭтвЛЖЏЕуЃЌЧв
Г§ЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЎШчЭМ
ЃЎШчЭМ![]() ЫљЪОЃЌЗжБ№вд
ЫљЪОЃЌЗжБ№вд![]() ЁЂ
ЁЂ![]() ЮЊБпЃЌ
ЮЊБпЃЌ
зїЕШБпШ§НЧаЮ![]() КЭЕШБпШ§НЧаЮ
КЭЕШБпШ§НЧаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЂйЧыевГіЭМжагы![]() ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЎ
ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЎ
ЂкжБНгаДГіЯпЖЮ![]() ГЄЕФзюДѓжЕЃЎ
ГЄЕФзюДѓжЕЃЎ
ЃЈ![]() ЃЉЁОЭиеЙЁПШчЭМ
ЃЉЁОЭиеЙЁПШчЭМ![]() ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу
ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ
![]() ЭтвЛЖЏЕуЃЌЧв
ЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЧыжБНгаДГіЯпЖЮ
ЃЎЧыжБНгаДГіЯпЖЮ![]() ГЄЕФзюДѓжЕМАДЫЪБЕу
ГЄЕФзюДѓжЕМАДЫЪБЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ




ЁОД№АИЁПЃЈ![]() ЃЉ
ЃЉ![]() бгГЄЯпЩЯЃЌ
бгГЄЯпЩЯЃЌ ![]() ЃЛЃЈ
ЃЛЃЈ![]() ЃЉЂй
ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЈ
ЃЈ![]() ЃЉ
ЃЉ![]() ЃЛ
ЃЛ ![]()
ЁОНтЮіЁПЃЈ![]() ЃЉЕБШ§ЕуВЛЙВЯпЪБЃЌШ§НЧаЮСНБпжЎКЭДѓгкЕкШ§БпЃЌМД
ЃЉЕБШ§ЕуВЛЙВЯпЪБЃЌШ§НЧаЮСНБпжЎКЭДѓгкЕкШ§БпЃЌМД![]() ЃЛ
ЃЛ
ЕБ![]() дк
дк![]() бгГЄЯпЩЯЪБЃЌ
бгГЄЯпЩЯЪБЃЌ ![]() ЃЛ
ЃЛ
ЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ ![]() ЃЎ
ЃЎ
ЙЪЕБ![]() дк
дк![]() бгГЄЯпЩЯЪБЃЌ
бгГЄЯпЩЯЪБЃЌ ![]() ШЁЕУзюДѓжЕЃЌЧвЮЊ
ШЁЕУзюДѓжЕЃЌЧвЮЊ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЂйвРЬтвтЕУ
ЃЉЂйвРЬтвтЕУ![]() ЃЌ
ЃЌ ![]() ЃЌРћгУЕШБпШ§НЧаЮУПИіНЧЖМЪЧ
ЃЌРћгУЕШБпШ§НЧаЮУПИіНЧЖМЪЧ![]() КЭНЧЕФЙиЯЕЕУ
КЭНЧЕФЙиЯЕЕУ![]() ЃЌ
ЃЌ
зюКѓИљОнБпНЧБпЖЈРэжЄУї![]() Ёе
Ёе![]() ЃЌ
ЃЌ
ДгЖјЭЦГі![]() ЃЎ
ЃЎ
ЂквђЮЊ![]() ЃЌЫљвдЯпЖЮ
ЃЌЫљвдЯпЖЮ![]() ЕФзюДѓжЕМД
ЕФзюДѓжЕМД![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ИљОнШ§НЧаЮСНБпжЎКЭДѓгкЕкШ§БпЃЌЫљвд![]() зюДѓЪБМД
зюДѓЪБМД![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЙВЯпЃЌ
Ш§ЕуЙВЯпЃЌ
ЕУЕН![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
ЙЪ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉШчЭМ1ЃЌвдЕу
ЃЉШчЭМ1ЃЌвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ ![]() ЮЊАыОЖзїЛЁЃЌНЛвдЕу
ЮЊАыОЖзїЛЁЃЌНЛвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ
![]() ЮЊАыОЖзїЕФЛЁгкЕу
ЮЊАыОЖзїЕФЛЁгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
Ыљвд![]() Ёе
Ёе![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
гЩЃЈ![]() ЃЉПЩжЊЃЌЕБЕу
ЃЉПЩжЊЃЌЕБЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЪБЃЌ
ЕФбгГЄЯпЩЯЪБЃЌ ![]() ШЁЕУзюДѓжЕЃЌ
ШЁЕУзюДѓжЕЃЌ
гжвђЮЊ![]() ЃЌЫљвдДЫЪБ
ЃЌЫљвдДЫЪБ![]() ШЁЕУзюДѓжЕЃЎ
ШЁЕУзюДѓжЕЃЎ
ШчЭМ2ЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЪБЃЌЙ§Еу
ЕФбгГЄЯпЩЯЪБЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
дк![]() жаЃЌгЩЙДЙЩЖЈРэЕУ
жаЃЌгЩЙДЙЩЖЈРэЕУ
![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЎ
ЃЎ
вђЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
гжвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
гжвђЮЊЕу![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
ЫљвдЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПеХРЯЪІгк2014Фъ2дТЗндкГрЗхФГЯиГЧТђСЫвЛЬзТЅЗПЃЌЕБЪБ(МД2дТЗн)дкХЉааНшСЫ9ЭђдЊзЁЗПДћПюЃЌДћПюЦкЯоЮЊ6ФъЃЌДгПЊЪМДћПюЕФЯТвЛИідТЦ№ж№дТГЅЛЙЃЌДћПюдТРћТЪЪЧ0.5%ЃЌУПдТЛЙПюЪ§ЖюЃНЦНОљУПдТгІЛЙЕФДћПюБОН№Ъ§ЖюЃЋдТРћЯЂЃЌдТРћЯЂЃНЩЯдТЫљЪЃДћПюБОН№Ъ§ЖюЁСдТРћТЪЃЎ
(1)ЧѓеХРЯЪІНшПюКѓЕквЛИідТгІЛЙПюЕФЪ§ЖюЃЛ
(2)МйЩшДћПюдТРћТЪВЛБфЃЌЧыаДГіеХРЯЪІНшПюКѓЕкn(nЪЧе§ећЪ§)ИідТЛЙПюЪ§ЖюpгыnжЎМфЕФКЏЪ§НтЮіЪН(ВЛБиЛЏМђ)ЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЧѓеХРЯЪІ2016Фъ7дТЗнгІЛЙПюЪ§ЖюЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+ax+a-2=0
ЃЈ1ЃЉШєИУЗНГЬгавЛИіЪЕЪ§ИљЮЊ1ЃЌЧѓaЕФжЕМАЗНГЬЕФСэвЛЪЕИљЃЎ
ЃЈ2ЃЉЧѓжЄЃКВЛТлaШЁКЮЪЕЪ§ЃЌИУЗНГЬЖМгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
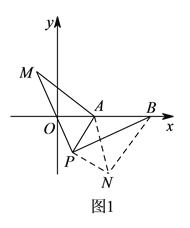
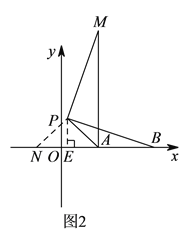
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНkxЃЋ6гыxжсЃЌyжсЗжБ№ЯрНЛгкЕуAЃЌBЃЌOЮЊзјБъдЕуЃЌЕуAЕФзјБъЮЊ(Ѓ8ЃЌ0)ЃЎ
(1)ЧѓkЕФжЕЃЛ
(2)ШєЕуP(xЃЌy)ЪЧЕкЖўЯѓЯоФкжБЯпЩЯЕФвЛИіЖЏЕуЃЌдкЕуPЕФдЫЖЏЙ§ГЬжаЃЌЪдаДГіЁїOPAЕФУцЛ§SгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
(3)ШєЕуP(0ЃЌm)ЮЊЩфЯпBO(BЃЌOСНЕуГ§Эт)ЩЯЕФвЛЖЏЕуЃЌЙ§ЕуPзїPCЁЭyжсНЛжБЯпABгкCЃЌСЌНгPA.ЩшЁїPACЕФУцЛ§ЮЊSЁфЃЌЧѓSЁфгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊx=5ЪЧЗНГЬaxЉ8=20+aЕФНтЃЌдђaЕФжЕЪЧЃЈЁЁЁЁЃЉ
A.2
B.3
C.7
D.8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЃЈaЉ1ЃЉ2+|bЉ2|=0ЃЌдђЃЈaЉbЃЉ2016ЕФжЕЪЧЃЈ ЃЉ
A.Љ1
B.1
C.0
D.2016
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2013ФъШЋЙњВЮМгИпПМЕФШЫЪ§ЮЊ9120000ШЫЃЌетИіЪ§зжгУПЦбЇМЧЪ§ЗЈБэЪОЪЧЃЈЁЁЁЁЃЉ
A.91.2ЁС105
B.9.12ЁС106
C.9.12ЁС107
D.0.912ЁС107
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁА*ЁБЪЧЙцЖЈЕФвЛжждЫЫуЗЈдђЃКa*b=a2Љ2bЃЎФЧУД2*3ЕФжЕЮЊЃЛШєЃЈЉ3ЃЉ*x=7ЃЌФЧУДx= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСадЫЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.x2+x3=x5
B.ЃЈx2ЃЉ3=x8
C.x6ЁТx2=x3
D.x4x2=x6
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com