
分析 将方程$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$=$\frac{3}{2}$两边同时平方可得$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{17}{4}$,由x2+y2=17可求得xy=4,运用完全平方公式可得x+y,x-y的值,由此可求出原方程组的解.
解答 解:将方程$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$=$\frac{3}{2}$两边同时平方可得,
$\frac{x}{y}$-2+$\frac{y}{x}$=$\frac{9}{4}$,
∴$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{17}{4}$.
∵x2+y2=17,
∴xy=4,
∴(x+y)2=x2+y2+2xy=25,
(x-y)2=x2+y2-2xy=9,
∴x+y=±5,x-y=±3.
解得$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=-1}\\{y=-4}\end{array}\right.$,$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$.
∵$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$=$\frac{3}{2}$>0,
∴原方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$.
点评 本题主要考查的是解方程组、完全平方公式等知识,将无理方程两边同时平方转化为整式方程,是解决本题的关键,本题是易错题,容易忽视隐含条件$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$>0.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
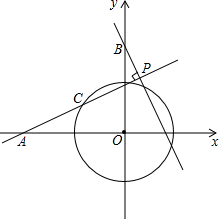 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为$\frac{1+\sqrt{3}}{2}$cm.
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为$\frac{1+\sqrt{3}}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com