
分析 (1)根据直角三角形中边角之间的关系,由c=7,∠A=36°,可以得到∠B的度数,从而可以求得其它的量,进而可以解答本题;
(2)根据直角三角形中边角之间的关系,由a=6,cosB=$\frac{\sqrt{5}-1}{2}$,可以得到c的值,从而可以取得其它的量,进而可以解答本题.
解答 解:(1)∵在Rt△ABC中,∠C=90°,c=7,∠A=36°,sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴∠B=90°-36°=54°,a=7×sin36°,b=7×cos36°.
∴a≈4.1,b≈5.7.
即∠B=54°,a≈4.1,b≈5.7.
(2))∵在Rt△ABC中,∠C=90°,a=6,cosB=$\frac{\sqrt{5}-1}{2}$,cosB=$\frac{a}{c}$,
∴c=$\frac{a}{cosB}=\frac{6}{\frac{\sqrt{5}-1}{2}}=\frac{12}{\sqrt{5}-1}=3\sqrt{5}+3$≈9.7.
∴b=$\sqrt{{c}^{2}-{a}^{2}}=\sqrt{(3\sqrt{5}+3)^{2}-{6}^{2}}$=$\sqrt{18+18\sqrt{5}}$≈7.6.
∵cosB=$\frac{\sqrt{5}-1}{2}$,
∴∠B≈55.389°=55°+0.389×60′=55°+23′+0.34×60″=55°23′+20.4″≈55°23′20″.
∴∠A=90°-55°23′20″=34°36′40″.
即b≈7.6,c≈9.7,∠A=34°36′40″,∠B=55°23′20″.
点评 本题考查解直角三角形,解题的关键是明确直角三角形中边角的关系.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
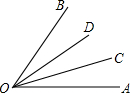 如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.
如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
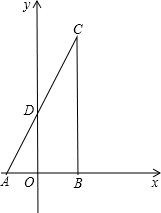 已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,
已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com