
【题目】如果点![]() 将线段
将线段![]() 分成两条相等的线段
分成两条相等的线段![]() 和
和![]() ,那么
,那么![]() 叫做线段
叫做线段![]() 的二等分点(中点);如果点
的二等分点(中点);如果点![]() ,
,![]() 将线段
将线段![]() 分成三条相等的线段
分成三条相等的线段![]() ,
,![]() 和
和![]() ,那么
,那么![]() ,
,![]() 叫做线段
叫做线段![]() 的三等分点;…;依此类推,如果点
的三等分点;…;依此类推,如果点![]() 将线段
将线段![]() 分成
分成![]() 条相等的线段
条相等的线段![]() ,那么
,那么![]() 叫做线段
叫做线段![]() 的
的![]() 等分点,如图①所示.
等分点,如图①所示.
已知点![]() 在直线
在直线![]() 的同侧,请回答下列问题.
的同侧,请回答下列问题.
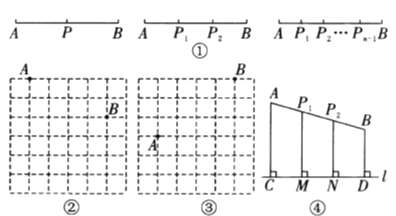
(1)在所给边长为![]() 个单位长度的正方形网格中,探究:
个单位长度的正方形网格中,探究:
①如图②,若点![]() 到直线
到直线![]() 的距离分别是4个单位长度和2个单位长度,则线段
的距离分别是4个单位长度和2个单位长度,则线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离是 个单位长度;
的距离是 个单位长度;
②如图③,若点![]() 到直线
到直线![]() 的距离分别是2个单位长度和5个单位长度,则线段
的距离分别是2个单位长度和5个单位长度,则线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离是 个单位长度;
的距离是 个单位长度;
③由①②可以发现结论:若点![]() 到直线
到直线![]() 的距离分别是
的距离分别是![]() 个单位长度和
个单位长度和![]() 个单位长度,则线段
个单位长度,则线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离是 个单位长度.
的距离是 个单位长度.
(2)如图④,若点![]() 到直线
到直线![]() 的距离分别是
的距离分别是![]() 和
和![]() ,利用(1)中的结论求线段
,利用(1)中的结论求线段![]() 的三等分点
的三等分点![]() ,
,![]() 到直线
到直线![]() 的距离分别是 .
的距离分别是 .
(3)若点![]() 到直线
到直线![]() 的距离分别是
的距离分别是![]() 和
和![]() ,点
,点![]() 为线段
为线段![]() 的
的![]() 等分点,直接写出第
等分点,直接写出第![]() 个
个![]() 等分点
等分点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1)①3;②![]() ;③
;③![]() ;(2)
;(2) ![]() ;(3)第
;(3)第![]() 个
个![]() 等分点
等分点![]() 到直线
到直线![]() 的距离:
的距离:![]() .
.
【解析】
(1)根据题意,在图②、图③中画出图形,观察,从而求得线段AB的中点到直线![]() 的距离与点A、B到直线
的距离与点A、B到直线![]() 的距离和的关系.
的距离和的关系.
(2)设P1M=x,由(1)中结论可得![]() =x,则P2N=2x-d1,由(1)中结论可得
=x,则P2N=2x-d1,由(1)中结论可得
![]() =P2N,即
=P2N,即![]() =2x-d1,易求即点1、P2到直线l的距离分别为
=2x-d1,易求即点1、P2到直线l的距离分别为
![]() 、
、![]() ;
;
(3)根据(1)、(2)的规律总结第i个n等分点Pi到直线l的距离.
(1)①如图②,AB在直线l的同侧,则线段AB的中点P到直线l的距离是![]() ×(4+2)=3(cm);
×(4+2)=3(cm);
故答案是:3;
②如图③,若点A.B到直线l的距离分别是2个单位和5个单位,那么线段AB的中点P到直线l的距离是:![]() =
=![]() (单位).
(单位).
故答案是:![]() ;
;
③由①②可以发现结论:若点A.B到直线l的距离分别是h个单位和t个单位,那么线段AB的中点P到直线l的距离是![]() 单位。
单位。
故答案是:![]() .
.
(2)如图(4),设P1M=x,由(1)中结论可得![]() =x,
=x,
∴P2N=2xd1,
由(1)中结论可得![]() =P2N,即
=P2N,即![]() =2xd1,
=2xd1,
解方程得x=![]() ,
,
∴P2N=![]() ,即点P1、P2到直线l的距离分别为
,即点P1、P2到直线l的距离分别为![]() 、
、![]() ,
,
若点A.B到直线l的距离分别是d1和d2,利用(1)中的结论求线段AB的三等分点P1、P2到直线l的距离![]() 、
、![]() .
.
(3)若点A.B到直线l的距离分别是d1和d2,点P1、P2、…Pn1为线段AB的n等分点,则第i个n等分点Pi到直线l的距离是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道1+2+3+…+![]() =
=![]() ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .
[问题提出] 那么 ![]() 的结果等于多少呢?
的结果等于多少呢?
[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+![]() n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
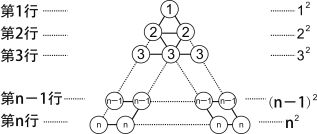
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.

图2
[问题解决]
(1).根据以上规律可得![]() __________________.
__________________.
(2).试计算 ![]() ,请写出计算步骤.
,请写出计算步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
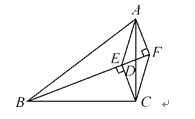
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题: 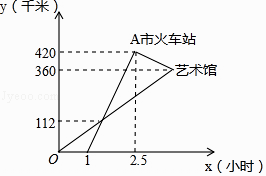
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) 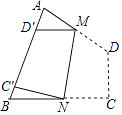
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com