
如图,函数y=
 的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )
的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )
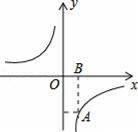

A.k=3 B.x<0时,y随x增大而增大
C.S△AOB=3 D.函数图象关于y轴对称
B【考点】反比例函数的性质.
【分析】首先把(1,﹣3)代入反比例函数关系式,可得k的值,进而可得A错误,根据反比例函数的性质:当k<0时,在每一个象限内,函数值y随自变量x增大而增大可得B正确,根据三角形的面积公式可C错误;根据反比例函数的性质可得D错误.
【解答】解:∵函数y=
 的图象经过点A(1,﹣3),
的图象经过点A(1,﹣3),
∴﹣3=
 ,
,
解得:k=﹣3,
故A错误;
∵k<0,
∴x<0时,y随x增大而增大,
故B正确;
∵点A(1,﹣3),AB垂直x轴于点B,
∴S△AOB=3×1×
 =
=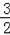
 ,
,
故C错误;
反比例函数图象关于原点对称,故D错误;
故选:B.
【点评】此题主要考查了反比例函数的性质,关键是掌握反比例函数的性质:
(1)反比例函数y=
 (k≠0)的图象是双曲线;
(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
注意:反比例函数的图象与坐标轴没有交点.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
(1)问题发现
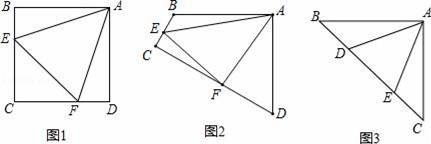
如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )


A.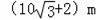
 B.
B.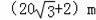
 C.
C.
 D.
D.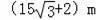

查看答案和解析>>
科目:初中数学 来源: 题型:
观察算式,探究规律:
当n=1时,S1=13=1=12;
当n=2时,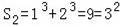
 ;
;
当n=3时,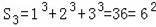
 ;
;
当n=4时,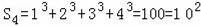
 ;
;
…
那么Sn与n的关系为( )
A.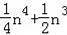
 B.
B.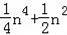
 C.
C.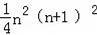
 D.
D.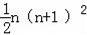

查看答案和解析>>
科目:初中数学 来源: 题型:
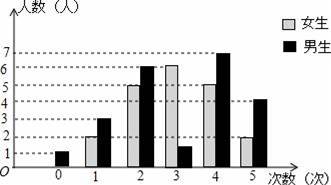
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
(1)该班级女生人数是 ;女生收看“两会”新闻次数的众数是 ;中位数是 .
(2)求女生收看次数的平均数.
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明计算出女生收看“两会”新闻次数的方差为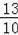
 ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
(4)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”,如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com