
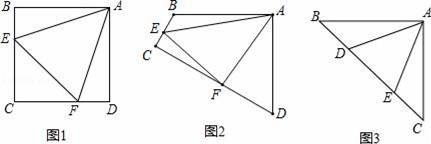
(1)问题发现
如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.

【考点】四边形综合题.
【分析】(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(3)把△ACE旋转到ABF的位置,连接DF,证明△AFE≌△AFG(SAS),则EF=FG,∠C=∠ABF=45°,△BDF是直角三角形,根据勾股定理即可作出判断.
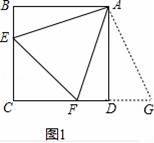
【解答】解:(1)理由是:如图1,

∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°﹣45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,
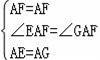
 ,
,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
(2)∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,
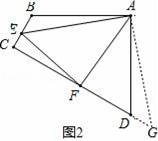

∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
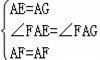
 ,
,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°;
(3)BD2+CE2=DE2.
理由是:把△ACE旋转到ABF的位置,连接DF,
则∠FAB=∠CAE.
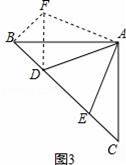

∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,
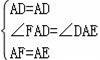
 ,
,
∴△ADF≌△ADE,
∴DF=DE,∠C=∠ABF=45°,
∴∠BDF=90°,
∴△BDF是直角三角形,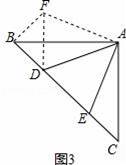

∴BD2+BF2=DF2,
∴BD2+CE2=DE2.
【点评】本题考查了全等三角形的性质和判定,正方形的性质的应用,解此题的关键是能正确作出辅助线得出全等三角形,综合性比较强,有一定的难度.


科目:初中数学 来源: 题型:
如图,△ABC中∠CAB的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F,作DM垂直于AB交AB于点M.
 (1)猜想CF和BM之间有何关系,并说明理由;
(1)猜想CF和BM之间有何关系,并说明理由;
(2)求证:AB-AC=2CF
查看答案和解析>>
科目:初中数学 来源: 题型:
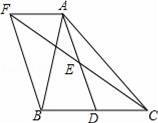
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(3)在(2)的条件下,△ABC满足条件 ,矩形AFBD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,函数y=
 的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )
的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )
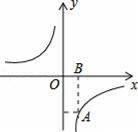

A.k=3 B.x<0时,y随x增大而增大
C.S△AOB=3 D.函数图象关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com