
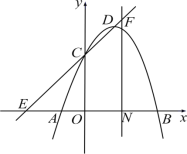
【题目】已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,直线CD与x轴交于点E.
(1)求A、B的坐标;
(2)求点E的坐标;
(3)过线段OB的中点N作x轴的垂线并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标(-1,0),点B的坐标(3,0);(2)(-3,0);(3)存在,(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)抛物线y=-x2+2x+3与x轴两个交点的横坐标即是方程-x2+2x+3=0的两个实数根;
(2)先根据二次函数表达式算出点C与顶点D,再用待定系数法算出直线CD的解析式,最后算出点E坐标即可;
(3)存在满足条件的点M(![]() ,m),过点M作MQ⊥CD于Q,连接OM,先证明Rt△FQM∽Rt△FNE,再利用相似的性质得到关于m的方程,解方程即可.
,m),过点M作MQ⊥CD于Q,连接OM,先证明Rt△FQM∽Rt△FNE,再利用相似的性质得到关于m的方程,解方程即可.
解:(1)由y=0得-x2+2x+3=0,
解得x1=-1,x2=3,
∴点A的坐标(-1,0),点B的坐标(3,0)
(2)由y=-x2+2x+3,令x=0,得y=3,
∴C(0,3)
又∵y=-x2+2x+3=-(x-1)2+4,
得D(1,4)
设直线CD的解析式为y=kx+b,得
![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为y=x+3
∴E(-3,0)
(3)存在.
由(1)(2)得,E(-3,0),N(![]() ,0)
,0)
∴F(![]() ,
, ![]() ),EN=
),EN=![]() ,
,
设存在满足条件的点M(![]() ,m),作MQ⊥CD于Q,则
,m),作MQ⊥CD于Q,则
FM=![]() , EF=
, EF=![]() , MQ=OM=
, MQ=OM=![]()
由题意得:Rt△FQM∽Rt△FNE,
∴![]() ,
,
∴4m2
∴m1= ![]() ,m2=
,m2=![]() ,
,
∴点M的坐标为M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() )
)



科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?
查看答案和解析>>
科目:初中数学 来源: 题型:
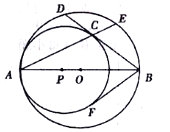
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 是半径
是半径![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为⊙
为⊙![]() 的半径,⊙
的半径,⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() .
.
(1)设![]() ,则
,则![]() 与
与![]() 之间的数量关系是什么?请说明理由.
之间的数量关系是什么?请说明理由.
(2)若![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,点
时,点![]() 是弦
是弦![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
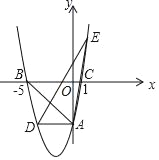
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣5交y轴于点A,交x轴于点B(﹣5,0)和点C(1,0),过点A作AD∥x轴交抛物线于点D.
(1)求此抛物线的表达式;
(2)点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,求△EAD的面积;
(3)若点P是直线AB下方的抛物线上一动点,当点P运动到某一位置时,△ABP的面积最大,求出此时点P的坐标和△ABP的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数![]() (k为常数)和一次函数
(k为常数)和一次函数![]() .
.
(1)求证:函数![]() 的图象与x轴有交点.
的图象与x轴有交点.
(2)已知函数![]() 的图象与x轴的两个交点间的距离等于3,
的图象与x轴的两个交点间的距离等于3,
①试求此时k的值.
②若![]() ,试求x的取值范围.
,试求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星星和阳阳是一对双胞胎,他们的爸爸买了两件不同图案的T恤给他们,星星和阳阳都想先挑选.于是阳阳设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的![]() 个小球,上面分别标有数字
个小球,上面分别标有数字![]() .一人先从袋中随机摸出一个小球,另一人再从袋中剩下的
.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的![]() 个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
(1)用树状图或列表法求出星星先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
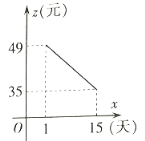
请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
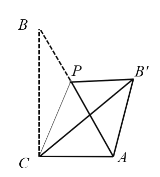
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
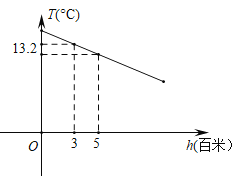
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com