
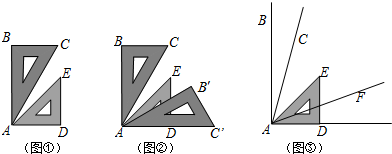
 解:(1)如图①,∵AB⊥AD,
解:(1)如图①,∵AB⊥AD,

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
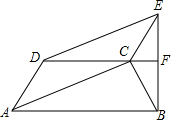 如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )
如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )| A、甲虫先到 | B、乙虫先到 |
| C、两虫同时到 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
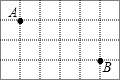 已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且△ABC为等腰三角形,则点C的个数为
已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且△ABC为等腰三角形,则点C的个数为查看答案和解析>>
科目:初中数学 来源: 题型:
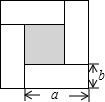 如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )| A、a2-b2=(a+b)(a-b) |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=(a+b)2-4ab |
| D、a2+ab=a(a+b) |
查看答案和解析>>
科目:初中数学 来源: 题型:
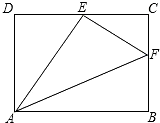 如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求:
如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com