
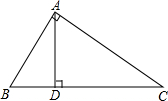
 在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.
在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长. 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
 如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?
如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,要测量池塘两端A,B的距离,先在平面上取一个可以直接到达A,B的点C,连接AC并延长到D,使AC=3CD,连接BC并延长到E,使BC=3CE,连接DE,测得DE=13m,那么池塘的宽AB是多少?
如图,要测量池塘两端A,B的距离,先在平面上取一个可以直接到达A,B的点C,连接AC并延长到D,使AC=3CD,连接BC并延长到E,使BC=3CE,连接DE,测得DE=13m,那么池塘的宽AB是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
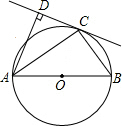 如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,C是⊙O上一点,AD与过C点的切线互相垂直,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com