
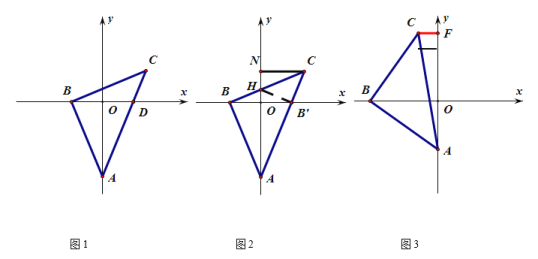
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��y�Ḻ�����ϵ�һ�����㣬��B��x�Ḻ�����ϵ�һ�����㣬����AB������B��AB�Ĵ��ߣ�ʹ��BC��AB���ҵ�C��x����Ϸ���
��1����֤����CBD����BAO��
��2����ͼ2����A����B�ڻ��������У���AB��y�ᷭ��ʹ��AB'�պ�����AC�ı��ϣ���ʱBC��y���ڵ�H������C��CN��ֱy���ڵ�N����֤AH��2CN��
��3����ͼ3����A����B�ڻ��������У�ʹ�õ�C�ڵڶ������ڣ�����C��CF��ֱy���ڵ�F����֤��OB��AO+CF��
���𰸡���1������������2������������3��������.
��������
��1������![]() ���Լ�
���Լ�![]() ��֤����CBD����BAO��
��֤����CBD����BAO��
��2���ӳ�CN��AB���ڵ�I�������۵�������֪��BAN����CAN�����֤����CAN����IAN������CN��NI����֤����ICB�ա�HAB�����ɵó�AH��2CN��
��3����C��CJ��ֱx�ᣬ����ΪJ��CJOFΪ��������CF��OJ�����ݡ�CBO+��BCJ����CBO+��OBA��900�ó���BCJ����OBA��֤����CBJ�ա�BAO������֤��OB��OA+CF.
�⣺��1����![]()
����CBD+��DBA����BAO+��DBA��900
���CBD����BAO
��2����ΪAB��y�ᷭ�ۿ�֪��
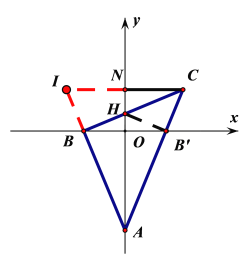
��BAN����CAN
�ӳ�CN��AB���ڵ�I��
�ڡ�CAN�͡�IAN��
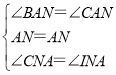
���CAN�ա�IAN��ASA��
��CN��NI
��CI��2CN
��CN��y��
���CNH����CBA��900
��BHA����NHC
���NCH����BAH
�ڡ�ICB�͡�HAB
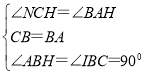
����ICB�ա�HAB��ASA��
��AH��CI
��AH��2CN
��3����C����CJ��ֱx�ᣬ����ΪJ��CJOFΪ������
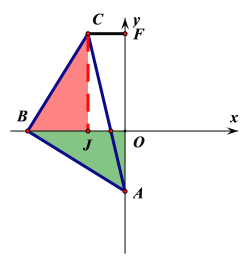
��CF��OJ
�ߡ�CBO+��BCJ����CBO+��OBA��900
���BCJ����OBA
�ڡ�CBJ�͡�BAO��
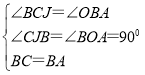
���CBJ�ա�BAO��AAS��
��BJ��OA
��OB��BJ+JO
��OB��OA+CF



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ڴ�����4����ȫ��ͬ��С�����Ƿֱ���Ϊ![]() ��
��
![]() �����ȡһ��С����ǡ���������Ϊ2��С��ĸ��ʣ�
�����ȡһ��С����ǡ���������Ϊ2��С��ĸ��ʣ�
![]() �����ȡһ��С��Ȼ��Żأ��������ȡһ��С�������б���������ͼ�������еĿ����ԣ�����������ȡ��С��ı�ŵĺ�Ϊ5�ĸ��ʣ�
�����ȡһ��С��Ȼ��Żأ��������ȡһ��С�������б���������ͼ�������еĿ����ԣ�����������ȡ��С��ı�ŵĺ�Ϊ5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����������������:��
����������������:��![]() ����
����![]() ����
����![]() �� ��
�� ��
A.ȫ����ȷB.���ٺ͢���ȷC.���ٺ���ȷD.���ٺ͢���ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
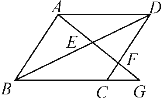
����Ŀ����ͼ����![]() ABCD�У���G��BC�ӳ�����һ�㣬AG��BD���ڵ�E����DC���ڵ�F����ͼ�����������ι��м��ԣ��ֱ�д������
ABCD�У���G��BC�ӳ�����һ�㣬AG��BD���ڵ�E����DC���ڵ�F����ͼ�����������ι��м��ԣ��ֱ�д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
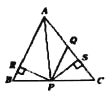
����Ŀ����ͼ�٣�����ABC�У���BAC=90����AB=AC��AO��BC�ڵ�O����F���߶�AO�ϵĵ�(��A��O���غ�)����EAF=90����AE=AF������FE��FC��BE��BF.
(1)��֤��BE=BF��
(2)��ͼ�ڣ�������AEF�Ƶ�A��ת��ʹ��AF�ڡ�BAC���ڲ����ӳ�CF��AB�ڵ�G����BE�ڵ�K.��֤����AGC�ס�KGB.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AD��BC���ϵ����ߣ���AB=10,AC=4,��AD��ȡֵ��Χ��_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ�DE��DF�ֱ�����ABD����ACD�ĸߣ��õ������ĸ����ۣ���OA=OD����AD��EF���۵���A=90��ʱ���ı���AEDF�������Σ���![]() ��������������ȷ����( )
��������������ȷ����( )
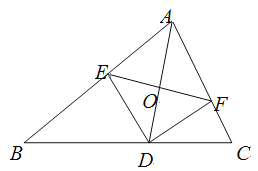
A. �ڢ� B. �ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ��㣩��ABC�Ķ���A��C������ֱ�Ϊ����4��5��������1��3��

��1����������ƽ��������ƽ��ֱ������ϵ����д��B���ꣻ
��2����������ABC����y��ԳƵ���A��B��C������д����B����C�������ꣻ
��3������ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com