
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
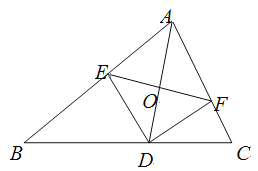
A. ②③ B. ②④ C. ①②③ D. ②③④
【答案】D
【解析】只要证明△ADE≌△ADF,推出AE=EF,DE=DF,推出AD垂直平分线段EF,即可判定②③正确,利用勾股定理即可判定④正确,①不一定成立故错误.
解:∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,
又∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF,
∴AD垂直平分EF,故②正确,
∵∠AED=∠AFD=90°,
∴当∠EAF=90°时,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,故③正确,
∵AE2+DF2=EO2+AO2+OD2+OF2,
DE2+AF2=OE2+OD2+OA2+OF2,
∴AE2+DF2=AF2+DE2,故④正确,
∵AD垂直平分EF,
而EF不一定垂直平分AD,故①错误,
故选D.


科目:初中数学 来源: 题型:
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
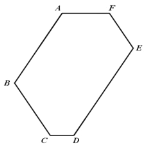
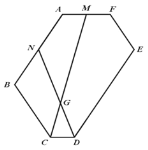
图 1 图 2
查看答案和解析>>
科目:初中数学 来源: 题型:
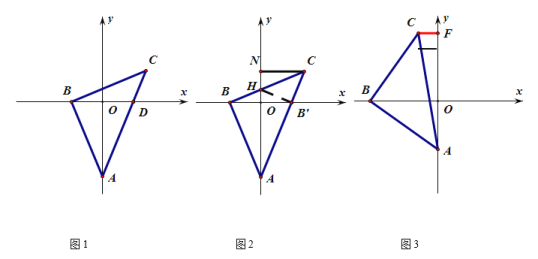
【题目】如图1,在平面直角坐标系中,点A是y轴负半轴上的一个动点,点B是x轴负半轴上的一个动点,连接AB,过点B作AB的垂线,使得BC=AB,且点C在x轴的上方.
(1)求证:∠CBD=∠BAO;
(2)如图2,点A、点B在滑动过程中,把AB沿y轴翻折使得AB'刚好落在AC的边上,此时BC交y轴于点H,过点C作CN垂直y轴于点N,求证AH=2CN;
(3)如图3,点A、点B在滑动过程中,使得点C在第二象限内,过点C作CF垂直y轴于点F,求证:OB=AO+CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c是△ABC的三条边,关于x的方程x2+2![]() x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
(1)求证:△ABC为等边三角形;
(2)若a,b为方程x2+mx-3m=0的两根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
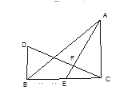
(1)求证.AE=CD;
(2)若BD=5㎝,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于A、B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则C点的坐标为( )
x+4与x轴、y轴分别交于A、B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则C点的坐标为( )

A.(4,0)B.(0,2)C.(0,1.5)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
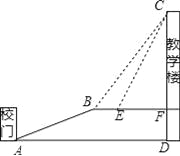
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i;(2)求DC的长.(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com