
【题目】设a、b、c是△ABC的三条边,关于x的方程x2+2![]() x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
(1)求证:△ABC为等边三角形;
(2)若a,b为方程x2+mx-3m=0的两根,求m的值.
【答案】(1)证明见解析;(2)m1=0,m2=-12.
【解析】试题分析:(1)根据关于x的方程x2+2![]() x+2c-a=0有两个相等的实数根可得△=0,即a+b-2c=0,由方程3cx+2b=2a的根为0可得2b=2a,至此可得a、b、c的数量关系,即可解决;
x+2c-a=0有两个相等的实数根可得△=0,即a+b-2c=0,由方程3cx+2b=2a的根为0可得2b=2a,至此可得a、b、c的数量关系,即可解决;
(2)由(1)得a=b,结合a、b为方程x2+mx-3m=0的两根可得m2+12m=0,解方程即可.
试题解析:(1)∵方程x2+2![]() x+2c-a=0有两个相等的实根,
x+2c-a=0有两个相等的实根,
∴△=0,即△=(2![]() )2-4×(2c-a)=0,
)2-4×(2c-a)=0,
解得a+b=2c,
∵方程3cx+2b=2a的根为0,
∴2b=2a,a=b,
∴2a=2c,a=c,
∴a=b=c,
故△ABC为等边三角形.
(2)∵a、b相等,
∴x2+mx-3m=0有两个相等的实根,
∴△=0,即△=m2+4×1×3m=0,
即m1=0,m2=-12,
.∵a、b为正数,
∴m1=0(舍),故m=-12.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】若 二 次 函 数 y ax bx c 的 图 象 与 x 轴 交 于 A 和 B 两 点 , 顶 点 为 C , 且b 4ac 4 ,则 ACB 的度数为()
A. 120° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,点F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连接FE,FC,BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.求证:△AGC∽△KGB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8![]() B. 8 C. 4
B. 8 C. 4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
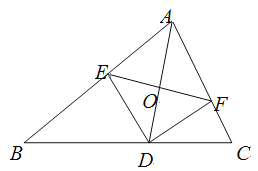
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“![]() ”方向排列,如
”方向排列,如![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 根据这个规律探索可得,第100个点的坐标为
根据这个规律探索可得,第100个点的坐标为![]()
![]()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com