练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知在△ABC中，AD是BC边上的中线，若AB=10,AC=4,则AD的取值范围是_____.

    【答案】3＜AD＜7

    【解析】

    连接AD并延长到点E，使DE=DA，连接BE，利用SAS证得△BDE≌△CDA，进而得到BE=CA=4，利用三角形两边之和大于第三边，两边之差小于第三边，即可求得AE的取值范围，进而求出AD的取值范围.

    如图，连接AD并延长到点E，使DE=DA，连接BE，

    ∵在△ABC中，AD是BC边上的中线

    ∴BD=CD

    在△BDE和△CDA中

    ∴△BDE≌△CDA（SAS）

    ∴BE=CA=4

    在△ABE中，AB+BE>AE，且AB﹣BE＜AE

    ∵AB=10,AC=4,

    ∴6＜AE＜14

    ∴3＜AD＜7

    故答案为3＜AD＜7

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我们做起”，小刚在他所在班的50名同学中，随机调查了10名同学家庭中的一年的月均用水量(单位：t)，其用水量分别为6、7、6.5、6.5、7.5、7.5、6.5、6、8、6.5.求这10个数据的平均数.众数.中位数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将长方形ABCD沿着对角线BD折叠，使点C落在处，交AD于点E．

    （1）试判断△BDE的形状，并说明理由；

    （2）若，，求△BDE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

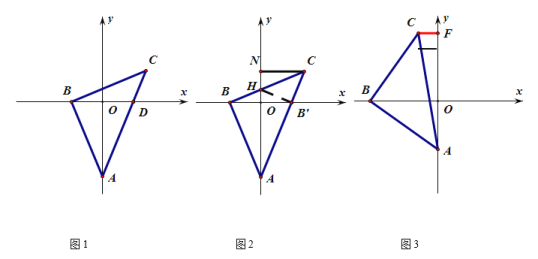
    【题目】如图1，在平面直角坐标系中，点A是y轴负半轴上的一个动点，点B是x轴负半轴上的一个动点，连接AB，过点B作AB的垂线，使得BC＝AB，且点C在x轴的上方．

    （1）求证：∠CBD＝∠BAO；

    （2）如图2，点A、点B在滑动过程中，把AB沿y轴翻折使得AB'刚好落在AC的边上，此时BC交y轴于点H，过点C作CN垂直y轴于点N，求证AH＝2CN；

    （3）如图3，点A、点B在滑动过程中，使得点C在第二象限内，过点C作CF垂直y轴于点F，求证：OB＝AO+CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为10，点E、F、G、H分别在AB、BC、CD、DA上，且满足AE∶BF∶CG∶DH=1∶2∶3∶4. 问当AE长为多少时，四边形EFGH的面积最小?并求出这个最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设a、b、c是△ABC的三条边,关于x的方程x2+2x+2c-a=0有两个相等的实数根，方程3cx+2b=2a的根为0.

    （1）求证：△ABC为等边三角形；

    （2）若a,b为方程x2+mx-3m=0的两根，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上．正确的是__．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】郴州市正在创建“全国文明城市”，某校拟举办“创文知识”抢答赛，欲购买A、B两种奖品以鼓励抢答者．如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元．

    （1）A、B两种奖品每件各多少元？

    （2）现要购买A、B两种奖品共100件，总费用不超过900元，那么A种奖品最多购买多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．

    （1）求证：GF=GC；

    （2）用等式表示线段BH与AE的数量关系，并证明．

    查看答案和解析>>

    同步练习册答案