
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)

 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
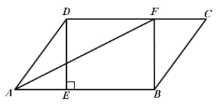
【题目】如图,在平行四边形 ABCD 中,过点 D 作 DE AB 于点 E ,点 F在边 CD 上, DF BE ,连接 AF , BF .
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分 DAB , CF3,BF4 ,求 DF 长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
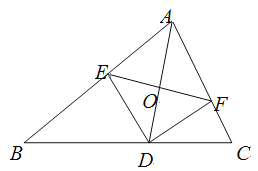
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:

(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
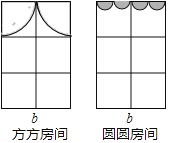
【题目】方方和圆圆房间的窗户的装饰物如图中的阴影部分,它们分别由两个四分之一圆和四个半圆组成(半径部分分别相同).求:
(1)方方房间窗户饰物的面积是 ,圆圆房间窗户饰物的面积是 .
(2)若长方形窗户的长为a,宽为b,请分别说明他们的窗户能射进阳光的面积是多少(窗框面积不计)?并说明谁的窗户射进阳光面积较大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com