
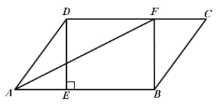
【题目】如图,在平行四边形 ABCD 中,过点 D 作 DE AB 于点 E ,点 F在边 CD 上, DF BE ,连接 AF , BF .
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分 DAB , CF3,BF4 ,求 DF 长.
【答案】(1)见解析;(2)5.
【解析】
(1)证DF=BE,DF∥BE,得四边形BFDE是平行四边形再由DE⊥AB,得四边形BFDE是矩形.
(2)根据勾股定理可求BC,由平行四边形性质得AD=BC,由等腰三角形性质得DF=AD.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE
∴四边形BFDE是平行四边形,
∵DE⊥AB
∴四边形BFDE是矩形,
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5 ,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )

A. R2﹣r2=a2 B. a=2Rsin36° C. a=2rtan36° D. r=Rcos36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过点A,C.
的图象经过点C,一次函数y=ax+b的图象经过点A,C.
(1)求反比例函数和一次函数的表达式;
(2)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我们做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中的一年的月均用水量(单位:t),其用水量分别为6、7、6.5、6.5、7.5、7.5、6.5、6、8、6.5.求这10个数据的平均数.众数.中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
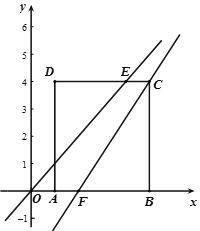
【题目】将边长为4的正方形ABCD置于平面直角坐标系中,使AB边落在x轴的正半轴上且A点的坐标是![]() ,直线y=x与线段CD交于点E.
,直线y=x与线段CD交于点E.
(1)直线![]() 经过点C且与
经过点C且与![]() 轴交于点F.求四边形AFCD的面积.
轴交于点F.求四边形AFCD的面积.
(2)若直线![]() 经过点E和点F,求直线
经过点E和点F,求直线![]() 的解析式.
的解析式.
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,将(2)中直线
平行,将(2)中直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点M,交直线
轴于点M,交直线![]() 于点N,求
于点N,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
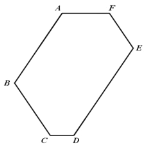
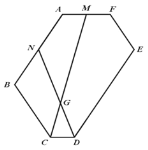
图 1 图 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
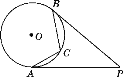
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com