
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过点A,C.
的图象经过点C,一次函数y=ax+b的图象经过点A,C.
(1)求反比例函数和一次函数的表达式;
(2)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求P点的坐标.

【答案】(1) y=-![]() , y=-x+2 ;(2) P点坐标为(25,-
, y=-x+2 ;(2) P点坐标为(25,-![]() )或(-25,
)或(-25,![]() ).
).
【解析】
试题(1)先根据条件求出点C的坐标,代入y=![]() 可求出k的值,把点A,C坐标代入一次函数解析式y=ax+b,然后解方程组可得a,b的值;(2)设点P的坐标为(x,y),根据△OAP的面积恰好等于正方形ABCD的面积,可求出点P的横坐标x,代入反比例函数关系式可求出点P的纵坐标.
可求出k的值,把点A,C坐标代入一次函数解析式y=ax+b,然后解方程组可得a,b的值;(2)设点P的坐标为(x,y),根据△OAP的面积恰好等于正方形ABCD的面积,可求出点P的横坐标x,代入反比例函数关系式可求出点P的纵坐标.
试题解析:(1) 因为四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),所以C的坐标为(5,-3),代入y=![]() 可得:k=-15,所以反比例函数的解析式为
可得:k=-15,所以反比例函数的解析式为![]() ;把点A,C坐标代入一次函数解析式得
;把点A,C坐标代入一次函数解析式得![]() ,解得
,解得![]() ,所以一次函数的解析式为y=-x+2;
,所以一次函数的解析式为y=-x+2;
(2) 设点P的坐标为(x,y),根据△OAP的面积恰好等于正方形ABCD的面积,得:![]() ,所以
,所以![]() ,代入
,代入![]() ,得
,得![]() 或
或![]() ,所以P点的坐标为(25,-
,所以P点的坐标为(25,-![]() )或(-25,
)或(-25,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
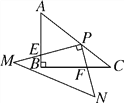
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
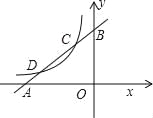
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有4个完全相同的小球,把它们分别标号为![]() .
.
![]() 随机摸取一个小球,求恰好摸到标号为2的小球的概率;
随机摸取一个小球,求恰好摸到标号为2的小球的概率;
![]() 随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法或树形图画出所有的可能性,并求两次摸取的小球的标号的和为5的概率.
随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法或树形图画出所有的可能性,并求两次摸取的小球的标号的和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD 中,过点 D 作 DE AB 于点 E ,点 F在边 CD 上, DF BE ,连接 AF , BF .
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分 DAB , CF3,BF4 ,求 DF 长.
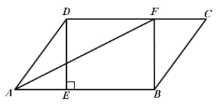
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com