
【题目】如图,P点坐标为(2,2),l1⊥l2,l1.l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为_______.

科目:初中数学 来源: 题型:
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0).
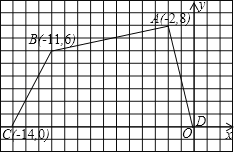
(1)求这个四边形的面积;
(2)如果把四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,所得的四边形的面积又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过点A,C.
的图象经过点C,一次函数y=ax+b的图象经过点A,C.
(1)求反比例函数和一次函数的表达式;
(2)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.(![]() ,
, ![]() ≈1.7,结果保留整数)
≈1.7,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我们做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中的一年的月均用水量(单位:t),其用水量分别为6、7、6.5、6.5、7.5、7.5、6.5、6、8、6.5.求这10个数据的平均数.众数.中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
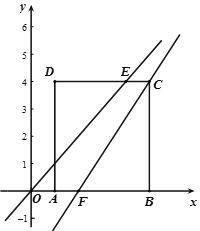
【题目】将边长为4的正方形ABCD置于平面直角坐标系中,使AB边落在x轴的正半轴上且A点的坐标是![]() ,直线y=x与线段CD交于点E.
,直线y=x与线段CD交于点E.
(1)直线![]() 经过点C且与
经过点C且与![]() 轴交于点F.求四边形AFCD的面积.
轴交于点F.求四边形AFCD的面积.
(2)若直线![]() 经过点E和点F,求直线
经过点E和点F,求直线![]() 的解析式.
的解析式.
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,将(2)中直线
平行,将(2)中直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点M,交直线
轴于点M,交直线![]() 于点N,求
于点N,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
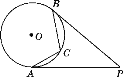
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F、G、H分别在AB、BC、CD、DA上,且满足AE∶BF∶CG∶DH=1∶2∶3∶4. 问当AE长为多少时,四边形EFGH的面积最小?并求出这个最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com