
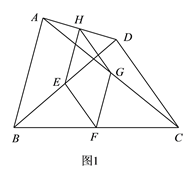
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
【答案】B
【解析】分析:A.用三角形的中位线定理判断四边形EFGH的形状;B.判断四边形EFGH的内角能否为直角;C.根据菱形的定义判断;D.当AD=3DH,BD=3DE,AC=3CG,BC=3CF时判断四边形EFGH是平行四边形.
详解:如图1,∵E,F,G,H分别是线段BD,BC,AC,AD的中点,
∴EF=![]() CD,FG=
CD,FG=![]() AB,GH=
AB,GH=![]() CD,HE=
CD,HE=![]() AB,
AB,
∴EF=GH,FG=HE,∴四边形EFGH为平行四边形.
则A正确;
如图2,当AC⊥BD时,∠1=90°,
∠1>∠2>∠EHG,∴四边形EHGF不可能是矩形,则B错误;

AB=CD,∴EF=FG=GH=HE,∴四边形EFGHB是菱形.
则C正确;
如图3,当E,F,H,G是相应线段的三等分点时,四边形EFGH是平行四边形.
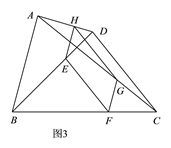
∵E,F,H,G是相应线段的三等分点,∴△EHD∽△BAD,△CFG∽△CBA,
![]() ,
, ![]() ,∴EH=FG,
,∴EH=FG,
又∵EH∥AB,FG∥AB,∴EH∥FG,
∴四边形EFGH是平行四边形,则D正确.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将边长为4的正方形ABCD置于平面直角坐标系中,使AB边落在x轴的正半轴上且A点的坐标是![]() ,直线y=x与线段CD交于点E.
,直线y=x与线段CD交于点E.
(1)直线![]() 经过点C且与
经过点C且与![]() 轴交于点F.求四边形AFCD的面积.
轴交于点F.求四边形AFCD的面积.
(2)若直线![]() 经过点E和点F,求直线
经过点E和点F,求直线![]() 的解析式.
的解析式.
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,将(2)中直线
平行,将(2)中直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点M,交直线
轴于点M,交直线![]() 于点N,求
于点N,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
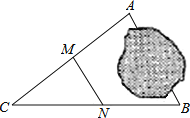
A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F、G、H分别在AB、BC、CD、DA上,且满足AE∶BF∶CG∶DH=1∶2∶3∶4. 问当AE长为多少时,四边形EFGH的面积最小?并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个大长方形剪去一个小长方形后形成的图形,已知动点P以2cm/s的速度沿图形边框按B-C-D-E-F-A的路径移动,相应的ΔABP的面积S(cm)与时间t(s)之间的关系如图,若AB=8cm,解答下列问题:


(1)BC的长是多少?
(2)图象中的a是几?
(3)六边形的面积是多少?
(4)图象中的b是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E,D分别是边AB,AC上的点,且AE=AD,BD,CE交于点F,AF的延长线交BC于点H,若∠EAF=∠DAF,则图中的全等三角形共有( )
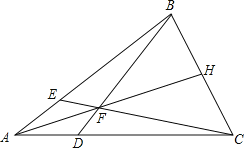
A.4对B.5对C.6对D.7对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com