练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图.在△ABC中，∠B=∠C=50°，D是BC的中点，DE⊥AB， DF⊥AC，则∠BAD=_________.

    【答案】40°

    【解析】

    据AAS易证得△BDE≌△CDF，可得ED=FD，据三角形全等的判定HL易证得△AED≌△AFD，即可得∠EAD=∠FAD，即AD为∠BAC的角平分线，即可得∠BAD的度数．

    ∵D是BC的中点，

    ∴BD=CD，

    ∵DE⊥AB，DF⊥AC，

    ∴∠BED=∠CFD=90°，

    又∵∠B=∠C=50°

    ∴△BDE≌△CDF(AAS)，

    ∴ED=FD；

    又∵∠AED=∠AFD=90°，AD为公共边，

    ∴△AED≌△AFD（HL），

    ∴∠EAD=∠FAD，即AD为∠BAC的角平分线，

    ∴∠BAD= (180°∠B∠C)= ×(180°50°50°)=40°.

    故答案填：40°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AB＝AC，AB的垂直平分线DE交AB、AC于点E、D，若△ABC和△BCD的周长分别为21cm和13cm，求△ABC的各边长．

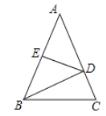
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ABD、∠ACD的角平分线交于点P，若∠A = 50°,∠D =10°，则∠P的度数为( )

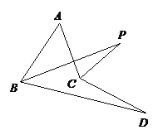
    A.15°B.20°C.25°D.30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在任意四边形ABCD中，AC，BD是对角线，E、F、G、H分别是线段BD、BC、AC、AD上的点，对于四边形EFGH的形状，某班的学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）

    A. 当E，F，G，H是各条线段的中点时，四边形EFGH为平行四边形

    B. 当E，F，G，H是各条线段的中点，且AC⊥BD时，四边形EFGH为矩形

    C. 当E，F，G，H是各条线段的中点，且AB=CD时，四边形EFGH为菱形

    D. 当E，F，G，H不是各条线段的中点时，四边形EFGH可以为平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，OA=OD，点F、D、O、A、E在同一直线上，AE=DF，求证：EB∥CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题情境）

    课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

    小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，连接BE．请根据小明的方法思考：

    （1）由已知和作图能得到△ADC≌△EDB，依据是　 　．

    A．SSS B．SAS C．AAS D．HL

    （2）由“三角形的三边关系”可求得AD的取值范围是　 　．

    解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．

    （初步运用）

    如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求线段BF的长．

    （灵活运用）

    如图3，在△ABC中，∠A＝90°，D为BC中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC中，∠ACB=90°，AC=BC=6，M点在边AC上，且CM=2，过M点作AC的垂线交AB边于E点，动点P从点A出发沿AC边向M点运动，速度为1个单位/秒，当动点P到达M点时，运动停止.连接EP、EC，设运动时间为t．在此过程中:

    （1）当t=1时，求EP的长度；

    （2）当t为何值时，△EPC是等腰三角形？

    （3）如图2，若点N是线段ME上一点，且MN=3，点Q是线段AE上一动点，连接PQ、PN、NQ得到△PQN，请直接写出△PQN周长的最小值.

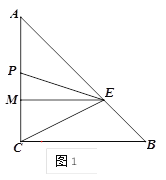
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E、F分别是矩形ABCD的边AD、AB上的点，EF=EC，且EF⊥EC．

    （1）求证：△AEF≌△DCE；

    （2）若DC=，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释. 如图1，有足够多的A类、C类正方形卡片和B类长方形卡片. 用若干张A类、B类、C类卡片可以拼出如图2的长方形，通过计算面积可以解释因式分解：．

    （1）如图3，用1张A类正方形卡片、4张B类长方形卡片、3张C类正方形卡片，可以拼出以下长方形，根据它的面积来解释的因式分解为________；

    （2）若解释因式分解，需取A类、B类、C类卡片若干张（三种卡片都要取到），拼成一个长方形，请画出相应的图形；

    （3）若取A类、B类、C类卡片若干张（三种卡片都要取到），拼成一个长方形，使其面积为，则m的值为________，将此多项式分解因式为________．

    查看答案和解析>>

    同步练习册答案