
����Ŀ����ƽ��ֱ������ϵ�У���֪A��B��������y=ax2��a��0����������ͬ�ĵ㣬����A�ڵڶ����ޣ�B�ڵ�һ���ޣ�
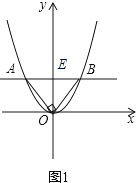
��1����ͼ1��ʾ����ֱ��AB��x��ƽ�У���AOB=90�㣬��AB=2ʱ����������ߵĽ���ʽ��A��B����ĺ�����ij˻���
��2����ͼ2��ʾ����1����õ��������ϣ���ֱ��AB��x�ƽ�У���AOB��Ϊ90��ʱ��A��B����ĺ�����ij˻��Ƿ�Ϊ����������ǣ������֤����������ǣ���˵�����ɣ�
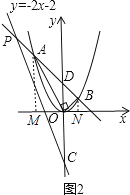
��3����2�������£���ֱ��y=��2x��2�ֱ�ֱ��AB��y���ڵ�P��C��ֱ��AB��y���ڵ�D���ҡ�BPC=��OCP�����P�����꣮
���𰸡�
��1��
����𡿽⣺��ͼ1����AB��x��ƽ�У�
���������ߵĶԳ�����AE=BE=1��
�ߡ�AOB=90�㣬
��OE=![]() AB=1��
AB=1��
��A����1��1����B��1��1����
��x=1ʱ��y=1����y=ax2�ã�a=1��
�������ߵĽ���ʽy=x2��
A��B����ĺ�����ij˻�ΪxAxB=��1
��2��
xAxB=��1������
��ͼ2����A��AM��x����M��BN��x����N��
���AMO=��BNO=90�㣬
���MAO+��AOM=��AOM+��BON=90�㣬
���MAO=��BON��
���AMO�ס�BON��
��![]() ��
��
��OMON=AMBN��
��A��xA��yA����B��xB��yB����
��A��xA��yA����B��xB��yB����y=x2ͼ���ϣ�
�࣬yA=![]() ��yB=
��yB=![]() ��
��
�ੁxAxB=yAyB=![]()
![]() ��
��
��xAxB=��1������
��3��
��A��m��m2����B��n��n2����
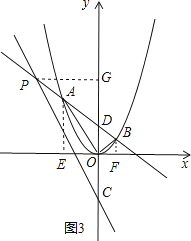
��ͼ3��ʾ������A��B�ֱ���x��Ĵ��ߣ�����ΪE��F������֤��AEO�ס�OFB��
��![]() ����
����![]() �������ã�mn��mn+1��=0��
�������ã�mn��mn+1��=0��
��mn��0����mn+1=0����mn=��1��
��ֱ��AB�Ľ���ʽΪy=kx+b������![]() ���ã�x2��kx��b=0��
���ã�x2��kx��b=0��
��m��n�Ƿ��̵�����������mn=��b��
��b=1��
��ֱ��AB��y�ύ�ڵ�D����OD=1��
��֪C��0����2����OC=2����CD=OC+OD=3��
�ߡ�BPC=��OCP����PD=CD=3��
��P��a����2a��2��������P��PG��y���ڵ�G����PG=��a��GD=OG��OD=��2a��3��
��Rt��PDG�У��ɹ��ɶ����ã�PG2+GD2=PD2��
��������a��2+����2a��3��2=32�������ã�5a2+12a=0��
���a=0����ȥ����a=![]() ��
��
��a=![]() ʱ����2a��2=
ʱ����2a��2=![]() ��
��
��P��![]() ��
��![]() ����
����
����������1����ͼ1����AB��x��ƽ�У����������ߵĶԳ�����AE=BE=1�����ڡ�AOB=90�㣬�õ�OE=![]() AB=1�����A����1��1����B��1��1������x=1ʱ��y=1����y=ax2�ã�a=1�õ������ߵĽ���ʽy=x2 �� A��B����ĺ�����ij˻�ΪxAxB=��1
AB=1�����A����1��1����B��1��1������x=1ʱ��y=1����y=ax2�ã�a=1�õ������ߵĽ���ʽy=x2 �� A��B����ĺ�����ij˻�ΪxAxB=��1
��2����ͼ2����A��AM��x����M��BN��x����N�õ���AMO=��BNO=90�㣬֤����AMO�ס�BON���õ�OMON=AMBN����A��xA �� yA����B��xB yB��������A��xA �� yA����B��xB �� yB����y=x2ͼ���ϣ��õ�yA=![]() ��yB=
��yB=![]() �����ɵõ����ۣ�
�����ɵõ����ۣ�
��3����A��m��m2����B��n��n2�����������ߣ�֤����AEO�ס�OFB���õ�mn=��1��������ֱ��m��y=kx+b��������y=x2�Ľ���ʽ���ɸ���ϵ����ϵ�õ���mn=��b������b=1���ɴ˵õ�OD��CD�ij��ȣ��Ӷ��õ�PD�ij��ȣ��������ߣ�����Rt��PDG���ɹ��ɶ��������P�����꣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��ԲO��ֱ����AB��AD��ԲO���ң���AB=AD������BC��DC�� 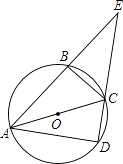
��1����֤����ABC�ա�ADC��
��2���ӳ�AB��DC���ڵ�E����EC=5cm��BC=3cm�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ����������P1��x1 �� y1����P2��x2 �� y2������|x1��x2|+|y1��y2|ΪP1��P2�����ֱ�Ǿ��룬������d��P1 �� P2����P0��2����3����һ���㣬Q��x��y����ֱ��y=kx+b�ϵ�һ���㣬��d��P0 �� Q������СֵΪP0��ֱ��y=kx+b��ֱ�Ǿ��룮��P��a����3����ֱ��y=x+1��ֱ�Ǿ���Ϊ6����a= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڸոձ�Ļ��2016ȫ�������ᡱ������������Ȼ����ό�㣬ij�м���Ϊ���˽���նԡ������������⡱�ľ۽��㣬��������˲��������Ե�����������������������ͼ��ʾ��ͳ��ͼ�������������� 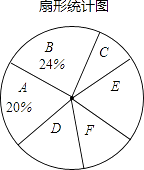
�l���ֲ���
��� | ���㻰�� | Ƶ���������� |
A | ҽ������ | 100 |
B | ʳƷ��ȫ | m |
C | ����ס�� | 40 |
D | ��ᱣ�� | 80 |
E | ��̬���� | n |
F | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m= �� n= �� ����ͳ��ͼ��E�飬F����ռ�İٷֱȷֱ�Ϊ��
��2�����������˿ڴ�Լ800������������й�עB�黰���������
��3��������ν��ܵ���������У�������һ�ˣ�����˹�עA�黰��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����1��1����B����3��1����C����1��4����
��1��������ABC����y��ԳƵġ�A1B1C1��
��2������ABC���ŵ�B˳ʱ����ת90���õ���A2BC2 �� ����ͼ�л�����A2BC2 �� ������߶�BC��ת��������ɨ�����������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=12cm��BC=18cm����P�ӵ�A������2cm/s���ٶ���A��D��C�˶�����P�ӵ�A������ͬʱ��Q�ӵ�C��������1cm/s���ٶ����B�˶�������P�����Cʱ����QҲֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
��1�����˶���ʼ����tȡ��ֵʱ��PQ��CD��
��2�����˶���ʼ����tȡ��ֵʱ����PQCΪֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����1�������1��������130Ԫ������2�������1��������180Ԫ��
��1����ÿ�������ÿ��������ۼۣ�
��2�����ijУ�ƻ�������������54�����ܷ��ò�����4000Ԫ������������ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2����
��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | a | 3.82 | 70% | 30% |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a= ��b= ��
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����25��ѧ����ѧ����ɼ�����λ���֣���Ƶ���ֲ�ֱ��ͼ��ͼ��
��1���ɼ�x��ʲô��Χ��������ࣿ�Ƕ����ˣ�
��2�����ð뾶Ϊ2������ͼ���������ɼ���60��x��70��������Ӧ����������Ƕ��٣�
��3������ɼ���50��x��60��90��x��100��ѧ������ѡ2�ˣ�С��ɼ���96�֣�����״ͼ���б����г����п��ܽ������С�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com