
【题目】在平面直角坐标系中,四边形OABC如图所示,点A在x轴负半轴上,BC∥AO(点B位于点C左侧),边BA、CO的延长线交于第三象限的点D,且DB=DC,若点B的横坐标是﹣4,AD:BD=1:3.
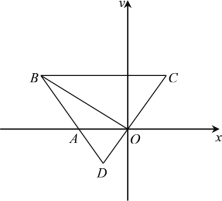
(1)求点A的坐标;
(2)连接OB,若△OBC是等腰三角形,求点C的坐标.
【答案】(1)点A的坐标为(﹣2,0);(2)C(2,2![]() )或C(2,4
)或C(2,4![]() ).
).
【解析】
(1)过点B作BE⊥x轴于点E,过点D作DF⊥x轴于点F,根据已知条件证明DF垂直平分AO,得到2AF+AE=4①,再根据DF∥BE,得到△ADF∽△ABE,得到![]() ,即AE=2AF②,再由①②得到AE=2,AF=1,故可得到A点坐标;
,即AE=2AF②,再由①②得到AE=2,AF=1,故可得到A点坐标;
(2)根据题意得到B、C两点关于直线x=﹣1对称,由B点横坐标为﹣4,得到C点横坐标为2,故BC=2﹣(﹣4)=6,再分两种情况讨论:当BO=BC时与OC=BC时,利用勾股定理进行求解.
(1)如图,过点B作BE⊥x轴于点E,过点D作DF⊥x轴于点F.
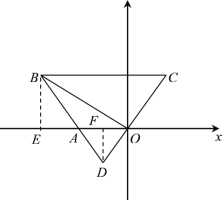
∵BC∥AO,
∴∠DBC=∠DAO,∠DCB=∠DOA
∵DB=DC
∴∠DAO =∠DOA
∴DA=DO 又∵DF⊥x轴
∴OF=AF,则2AF+AE=4①.
∵DF∥BE,
∴△ADF∽△ABE,
∴![]() ,即AE=2AF②,
,即AE=2AF②,
①与②联立,解得AE=2,AF=1,
∴点A的坐标为(﹣2,0);
(2)由题意得∠OAB>90°,OB>AB=OC,
∵DA=DO,DB=DC
∴B、C两点关于直线x=﹣1对称,B点横坐标为﹣4,
∴C点横坐标为2,
∴BC=2﹣(﹣4)=6.
∴当△OBC是等腰三角形时,分两种情况讨论:
①当BO=BC时,设B(﹣4,y1),
则16+![]() =36,解得y1=±2
=36,解得y1=±2![]() (负值舍去).
(负值舍去).
∴C(2,2![]() );
);
②当OC=BC时,设C(2,y2),
则4+![]() =36,解得y2=±4
=36,解得y2=±4![]() (负值舍去).
(负值舍去).
∴C(2,4![]() ).
).
∴C(2,2![]() )或C(2,4
)或C(2,4![]() ).
).


科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:①将半径2的⊙O六等分,依次得到A,B,C,D,E,F六个分点; ②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案是_________
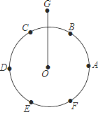
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b>0;③-1≤ a ≤-![]() ;④4ac-b2>8a;(5)3a+c=0,其中正确的结论有( )个
;④4ac-b2>8a;(5)3a+c=0,其中正确的结论有( )个
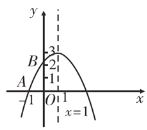
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量![]() (千克)与每千克降价
(千克)与每千克降价![]() (元)
(元)![]() 之间满足一次函数关系,其图象如图所示:
之间满足一次函数关系,其图象如图所示:
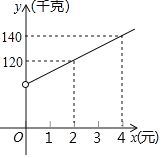
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
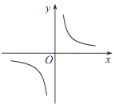
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.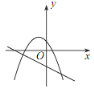 B.
B.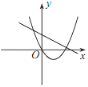 C.
C.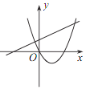 D.
D.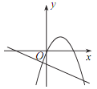
查看答案和解析>>
科目:初中数学 来源: 题型:
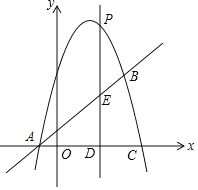
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=4,BC=6,点E为线段AB上一动点(不与点A. 点B重合),先将矩形ABCD沿CE折叠,使点B落在点F处,CF交AD于点H.
(1)求证:△AEG∽△DHC;
(2)若折叠过程中,CF与AD的交点H恰好是AD的中点时,求tan∠BEC的值;
(3)若折叠后,点B的对应F落在矩形ABCD的对称轴上,求此时AE的长.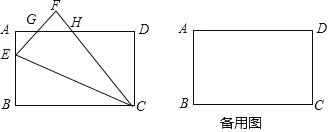
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com