
【题目】安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量![]() (千克)与每千克降价
(千克)与每千克降价![]() (元)
(元)![]() 之间满足一次函数关系,其图象如图所示:
之间满足一次函数关系,其图象如图所示:
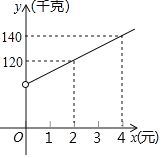
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=![]() ,AD=12.
,AD=12.
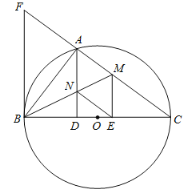
(1)求证:△ABF∽△ACB;
(2)求证:FB是⊙O的切线;
(3)证明四边形AMEN是菱形,并求该菱形的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
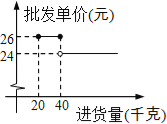
【题目】荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.
(1)请直接写出批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式;
(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种笔记本,进价为每本10元.试营销阶段发现:当销售单价为12元时,每天可卖出100本,如调整价格,每涨价1元,每天要少卖出10本.设该笔记本的销售单价为![]() 元,每天获得的销售利润为
元,每天获得的销售利润为![]() 元.
元.
(1)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当![]() 时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
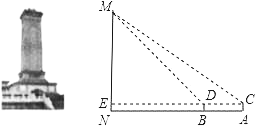
【题目】某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度,方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN项部M的仰角为37°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E.请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan35°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
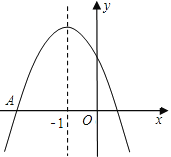
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com