
【题目】已知,如图,在矩形ABCD中,AB=4,BC=6,点E为线段AB上一动点(不与点A. 点B重合),先将矩形ABCD沿CE折叠,使点B落在点F处,CF交AD于点H.
(1)求证:△AEG∽△DHC;
(2)若折叠过程中,CF与AD的交点H恰好是AD的中点时,求tan∠BEC的值;
(3)若折叠后,点B的对应F落在矩形ABCD的对称轴上,求此时AE的长.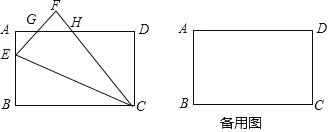
【答案】(1)见解析;(2)3 (3)![]() 或
或![]() .
.
【解析】
(1)根据矩形的性质得到CD=AB=4,AD=BC=6,∠A=∠B=∠D=90°,根据折叠的性质得到∠F=∠B=90°,根据余角的性质得到∠AEG=∠DHC,于是得到结论;
(2)由点H是AD的中点,得到AH=DH=3,根据相似三角形的性质得到GH=![]() ,得到AG=AD-GH-DH=
,得到AG=AD-GH-DH=![]() ,BE=2,根据三角函数的定义即可得到结论;
,BE=2,根据三角函数的定义即可得到结论;
(3)分两种情况考虑:F在横对称轴上与F在竖对称轴上,分别求出BF的长即可.
(1)∵在矩形ABCD中,AB=4,BC=6,
∴CD=AB=4,AD=BC=6,∠A=∠B=∠D=90°,
∵将矩形ABCD沿CE折叠,使点B落在点F处,
∴∠F=∠B=90°,
∵∠AGE=∠FGH,∠FHG=∠DHC,
∵∠FGH+∠FHG=90°,
∴∠AGE+∠DHC=90°,
∵∠AEG+∠AGE=90°,
∴∠AEG=∠DHC,
∴△AEG∽△DHC;
(2)∵点H是AD的中点,
∴AH=DH=3,
∵CD=4,
∴CH=5,FH=1,
∵∠F=∠D=90°,∠FHG=∠DHC,
∴△FHG∽△DHC,
∴![]() ,
,
∴GH=![]() ,
,
∴AG=ADGHDH=![]() ,
,
∵△AEG∽△DHC,
∴![]() ,
,
∴AE=1,
∴BE=2,
∴tan∠BEC=![]() =3,
=3,

(3)当F在横对称轴MN上,如图2所示,此时CN=![]() CD=2,CF=BC=6,
CD=2,CF=BC=6,
∴FN=![]() ,
,
∴MF=![]() ,
,
由折叠得,EF=BE,EM=2BE,
∴![]() ,
,
即![]() ,
,
∴BE=![]() ,
,
![]()

当F在竖对称轴MN上时,如图3所示,此时AB∥MN∥CD,
∴∠BEC=∠FOE,
∵∠BEC=∠FEC,
∴∠FEC=∠FOE,
∴EF=OF,
由折叠的性质得,BE=EF,∠EFC=∠B=90°,
∵BN=CN,
∴OC=OE,
∴FO=OE,
∴△EFO是等边三角形,
∴∠FEC=60°,
∴∠BEC=60°,
∴BE=![]() BC=
BC=![]() ,
,
∴AE=![]() .
.
综上所述,点B的对应F落在矩形ABCD的对称轴上,此时AE的长是![]() 或
或![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形OABC如图所示,点A在x轴负半轴上,BC∥AO(点B位于点C左侧),边BA、CO的延长线交于第三象限的点D,且DB=DC,若点B的横坐标是﹣4,AD:BD=1:3.
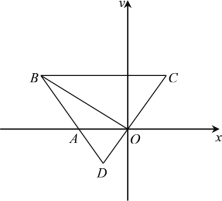
(1)求点A的坐标;
(2)连接OB,若△OBC是等腰三角形,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了提升菜篮子工程质量,计划用大、中型车辆共![]() 辆调拨不超过
辆调拨不超过![]() 吨蔬菜和
吨蔬菜和![]() 吨肉制品补充当地市场.已知一辆大型车可运蔬菜
吨肉制品补充当地市场.已知一辆大型车可运蔬菜![]() 吨和肉制品
吨和肉制品![]() 吨;一辆中型车可运蔬菜
吨;一辆中型车可运蔬菜![]() 吨和肉制品
吨和肉制品![]() 吨.
吨.
(1)符合题意的运输方案有几种?请你帮助设计出来;
(2)若一辆大型车的运费是![]() 元,一辆中型车的运费为
元,一辆中型车的运费为![]() 元,试说明
元,试说明![]() 中哪种运输方案费用最低?最低费用是多少元?
中哪种运输方案费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
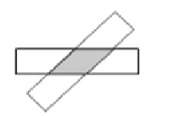
【题目】如图,将两张长为9,宽为3的矩形纸条交叉放置,其中重叠部分![]() 是一个菱形,则重叠部分菱形
是一个菱形,则重叠部分菱形![]() 周长最小值是__________,周长最大值是__________.
周长最小值是__________,周长最大值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件求二次函数解析式
(1)已知一个二次函数的图象经过了点A(0,﹣1),B(1,0),C(﹣1,2);
(2)已知抛物线顶点P(﹣1,﹣8),且过点A(0,﹣6);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y =![]() (x>0)的图象上,过点A作AC⊥x轴,垂足是C,一次函数y =kx+b的图象经过点A,与y轴的正半轴交于点B,AC =OC =2OB.
(x>0)的图象上,过点A作AC⊥x轴,垂足是C,一次函数y =kx+b的图象经过点A,与y轴的正半轴交于点B,AC =OC =2OB.

(1)求点A的坐标;
(2)求一次函数的表达式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有△ABC和△DEF.
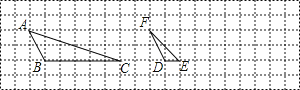
(1)这两个三角形相似吗?为什么?
(2)请直接写出∠A的度数 ;
(3)在上边的网格内再画一个三角形,使它与△ABC相似,并求出其相似比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com