
【题目】如图,在正方形网格上有△ABC和△DEF.
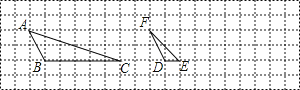
(1)这两个三角形相似吗?为什么?
(2)请直接写出∠A的度数 ;
(3)在上边的网格内再画一个三角形,使它与△ABC相似,并求出其相似比.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=4,BC=6,点E为线段AB上一动点(不与点A. 点B重合),先将矩形ABCD沿CE折叠,使点B落在点F处,CF交AD于点H.
(1)求证:△AEG∽△DHC;
(2)若折叠过程中,CF与AD的交点H恰好是AD的中点时,求tan∠BEC的值;
(3)若折叠后,点B的对应F落在矩形ABCD的对称轴上,求此时AE的长.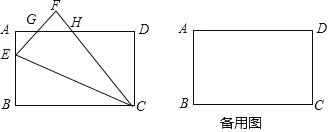
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2 + 1=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1,x2,且满足![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
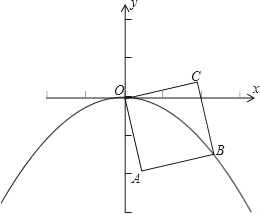
A. ![]() B.
B. ![]() C. ﹣2 D.
C. ﹣2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
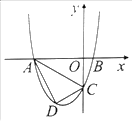
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax2+bx+c=0(a≠0),下列说法:①若方程有两个互为相反数的实数根,则b=0;②若方程ax2+bx+c=0没有实数根,则方程ax2+bx﹣c=0必有两个不相等的实根;③若二次三项式ax2+bx+c是完全平方式,则b2﹣4ac=0;④若c=0,则方程必有两个不相等的实数根.其中正确的是( )
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
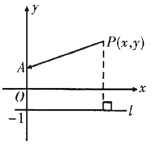
【题目】阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
问题:已知点![]() ,
,![]() ,直线
,直线![]() ,连接
,连接![]() ,若点
,若点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,请求出
的长相等,请求出![]() 与
与![]() 的关系式.
的关系式.
解:如图,∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,直线
,直线![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]()
∵点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,
的长相等,
∴![]() ,
,
平方化简得,![]() .
.
若将上述问题中![]() 点坐标改为
点坐标改为![]() ,直线
,直线![]() 变为
变为![]() ,按照问题解题思路,试求出
,按照问题解题思路,试求出![]() 与
与![]() 的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
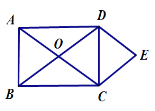
(1)试判断四边形OCED的形状,并说明理由;
(2)若∠DOC = 60°,BC = 6,求矩形ABCD的对角线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com