
【题目】如图所示,四边形![]() 为正方形,
为正方形,![]() 为
为![]() 上一点,将正方形折叠,使点
上一点,将正方形折叠,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() .求:
.求:
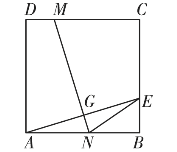
(1)![]() 的面积;
的面积;
(2)![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由tan∠AEN=![]() ,DC+CE=10可得出BE=
,DC+CE=10可得出BE=![]() AB,再由翻折变换的性质得出∠AEN=∠EAN,所以可以先设BE=a,从而求出AB=3a,CE=2a进而求出a的值, 由a的值可得出AB=6,CE=4.求出底AD的长,然后再由tan∠AEN与边的关系,求出高,最后利用面积公式求面积;
AB,再由翻折变换的性质得出∠AEN=∠EAN,所以可以先设BE=a,从而求出AB=3a,CE=2a进而求出a的值, 由a的值可得出AB=6,CE=4.求出底AD的长,然后再由tan∠AEN与边的关系,求出高,最后利用面积公式求面积;
(2)sin∠ENB的值用正弦定义求即可.
解:(1)由折叠可知:MN为AE的垂直平分线,
∴AN=EN,
∴∠EAN=∠AEN(等边对等角),
∴tan∠AEN=tan∠EAN=![]() ,
,
∴设BE=a,AB=3a,则CE=2a,
∵DC+CE=10,
∴3a+2a=10,
∴a=2,
设MN与AE交于点G,
∵由(1)知a=2,
∴AB=6,CE=4,
∵AE=![]() ,
,
∴EG=![]() AE=
AE=![]() ×2
×2![]() =
=![]() ,
,
又∵![]() ,
,
∴NG=![]() ,
,
∴AN=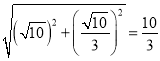 ,
,
∴AN=NE=![]() ,
,
∴S△ANE=![]() ;
;
(2)∵Rt△ENB中,EB=2,NE=![]() ,
,
∴sin∠ENB=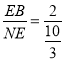 =
=![]() .
.


科目:初中数学 来源: 题型:
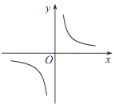
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.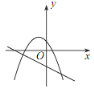 B.
B.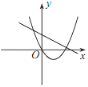 C.
C.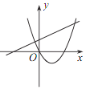 D.
D.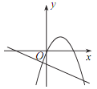
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=4,BC=6,点E为线段AB上一动点(不与点A. 点B重合),先将矩形ABCD沿CE折叠,使点B落在点F处,CF交AD于点H.
(1)求证:△AEG∽△DHC;
(2)若折叠过程中,CF与AD的交点H恰好是AD的中点时,求tan∠BEC的值;
(3)若折叠后,点B的对应F落在矩形ABCD的对称轴上,求此时AE的长.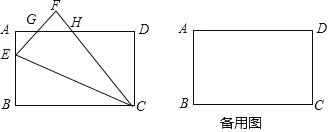
查看答案和解析>>
科目:初中数学 来源: 题型:
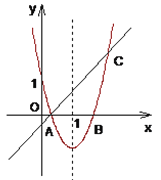
【题目】如图,一次函数![]() 与
与![]() 轴交点
轴交点![]() 恰好是二次函数与
恰好是二次函数与![]() 的其中一个交点,已知二次函数图象的对称轴为
的其中一个交点,已知二次函数图象的对称轴为![]() ,并与
,并与![]() 轴的交点为
轴的交点为![]() .
.
(1)求二次函数的解析式;
(2)设该二次函数与一次函数的另一个交点为![]() 点,连接
点,连接![]() ,求三角形
,求三角形![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,二次函数 y=x2+2x+2k﹣2 的图象与 x 轴有两个交点.
(1)求 k 的取值范围;
(2)当 k 取正整数时,请你写出二次函数 y=x2+2x+2k﹣2 的表达式,并求出此二次函数图象与 x 轴的两个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F,AB=6cm,AD=8cm.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.判断四边形FBGD的形状,并说明理由.
(3)在(2)的条件下,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2 + 1=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1,x2,且满足![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
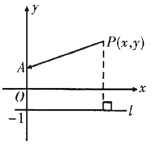
问题:已知点![]() ,
,![]() ,直线
,直线![]() ,连接
,连接![]() ,若点
,若点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,请求出
的长相等,请求出![]() 与
与![]() 的关系式.
的关系式.
解:如图,∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,直线
,直线![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]()
∵点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,
的长相等,
∴![]() ,
,
平方化简得,![]() .
.
若将上述问题中![]() 点坐标改为
点坐标改为![]() ,直线
,直线![]() 变为
变为![]() ,按照问题解题思路,试求出
,按照问题解题思路,试求出![]() 与
与![]() 的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com