
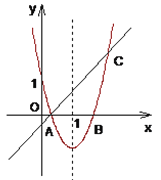
【题目】如图,一次函数![]() 与
与![]() 轴交点
轴交点![]() 恰好是二次函数与
恰好是二次函数与![]() 的其中一个交点,已知二次函数图象的对称轴为
的其中一个交点,已知二次函数图象的对称轴为![]() ,并与
,并与![]() 轴的交点为
轴的交点为![]() .
.
(1)求二次函数的解析式;
(2)设该二次函数与一次函数的另一个交点为![]() 点,连接
点,连接![]() ,求三角形
,求三角形![]() 的面积。
的面积。
【答案】(1) y=![]() x2
x2![]() x+1;(2)
x+1;(2)![]()
【解析】试题(1)先求得A的坐标为(![]() ,0),设二次函数的解析式为y=ax2+bx+1,二次函数图象的对称轴为x=1,且过A(
,0),设二次函数的解析式为y=ax2+bx+1,二次函数图象的对称轴为x=1,且过A(![]() ,0),列出方程组解得a、b的值即可;
,0),列出方程组解得a、b的值即可;
(2)先求当y=0时,![]() x2
x2![]() x+1=0解得x1=
x+1=0解得x1=![]() ,x2=
,x2=![]() ,求得B(
,求得B(![]() ,0),由
,0),由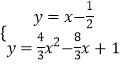 解得
解得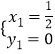 ;
;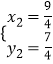 ,故C(
,故C(![]() ,
,![]() ),即可求得三角形ABC的面积.
),即可求得三角形ABC的面积.
试题解析:(1)由已知可得y=x-![]() 与x轴交点A的坐标为(
与x轴交点A的坐标为(![]() ,0)
,0)
∵二次函数过(0,1)
∴设二次函数的解析式为y=ax2+bx+1
∵二次函数图象的对称轴为x=1,且过A(![]() ,0)
,0)
故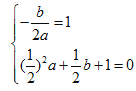 解得
解得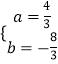
∴二次函数的解析式为:y=![]() x2
x2![]() x+1;
x+1;
(2)由(1)知函数y=![]() span>x2
span>x2![]() x+1过A(
x+1过A(![]() ,0),
,0),
当y=0时,![]() x2
x2![]() x+1=0解得x1=
x+1=0解得x1=![]() ,x2=
,x2=![]() ,
,
故B(![]() ,0)
,0)
由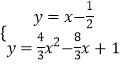 解得
解得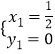 ;
;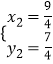 ,
,
故C(![]() ,
,![]() )
)
∴S△ABC=![]() ×(
×(![]() -
-![]() )×
)×![]() =
=![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件求二次函数解析式
(1)已知一个二次函数的图象经过了点A(0,﹣1),B(1,0),C(﹣1,2);
(2)已知抛物线顶点P(﹣1,﹣8),且过点A(0,﹣6);
查看答案和解析>>
科目:初中数学 来源: 题型:
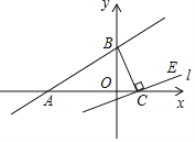
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0)、B(0,6),过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.
(1)求一次函数y=kx+b(k≠0)的解析式;
(2)求直线l的解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com