
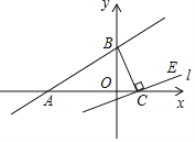
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0)、B(0,6),过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.
(1)求一次函数y=kx+b(k≠0)的解析式;
(2)求直线l的解析式;
【答案】(1)y=![]() x+6;(2)y=
x+6;(2)y=![]() x﹣
x﹣![]() ;
;
【解析】
(1)利用待定系数法求出直线表达式;
(2)记直线l与y轴的交点为D,再证明△OBC∽△OCD可得![]() ,由此可得D、C坐标,即可得直线l的解析式.
,由此可得D、C坐标,即可得直线l的解析式.
解:(1)∵一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0),B(0,6)两点,
∴![]()
∴![]()
∴一次函数y=kx+b的表达式为y=![]() x+6;
x+6;
(2)如图,记直线l与y轴的交点为D,
∵BC⊥l,
∴∠BCD=90°=∠BOC,
∴∠OBC+∠OCB=∠OCD+∠OCB,
∴∠OBC=∠OCD,
∵∠BOC=∠COD,
∴△OBC∽△OCD,
∴![]()
∵B(0,6),C(2,0),
∴OB=6,OC=2,
∴![]()
∴OD=![]()
∴D(0,﹣![]() ),
),
∵C(2,0),
∴直线l的解析式为y=![]() x﹣
x﹣![]()


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, AB=AC=10,线段BC在![]() 轴上,BC=12,点B的坐标为(-3,0),线段AB交
轴上,BC=12,点B的坐标为(-3,0),线段AB交![]() 轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿
轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿![]() 轴向右运动,设运动的时间为
轴向右运动,设运动的时间为![]() 秒.
秒.
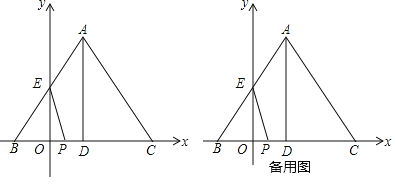
(1)当△BPE是等腰三角形时,求![]() 的值;
的值;
(2)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切时,求![]() 的值和此时点C的坐标.
的值和此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设![]() 为三角形三边,
为三角形三边,![]() 为面积,则
为面积,则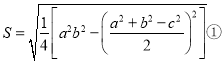 ,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设
,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设![]() (周长的一半),则
(周长的一半),则![]()
(1)尝试验证.这两个公式在表面上形式很不一致,请你用以![]() 为三边构成的三角形,分别验证它们的面积值;
为三边构成的三角形,分别验证它们的面积值;
(2)问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从![]() 或者
或者![]() );
);
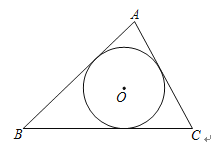
(3)问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图,![]() 的内切圆半径为
的内切圆半径为![]() ,三角形三边长为
,三角形三边长为![]() ,仍记
,仍记![]() ,
,![]() 为三角形面积,则
为三角形面积,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:线段![]()
(1)请用尺规作一个菱形![]() ,使它的两条对角线
,使它的两条对角线![]() ,
,![]() .
.
(注意:不能在已知线段上作图,要求保留作图痕迹,不写作法)
(2)若![]() ,
,![]() ,求:菱形
,求:菱形![]() 的面积?
的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
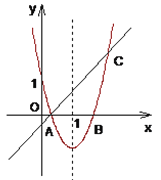
【题目】如图,一次函数![]() 与
与![]() 轴交点
轴交点![]() 恰好是二次函数与
恰好是二次函数与![]() 的其中一个交点,已知二次函数图象的对称轴为
的其中一个交点,已知二次函数图象的对称轴为![]() ,并与
,并与![]() 轴的交点为
轴的交点为![]() .
.
(1)求二次函数的解析式;
(2)设该二次函数与一次函数的另一个交点为![]() 点,连接
点,连接![]() ,求三角形
,求三角形![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
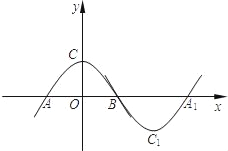
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
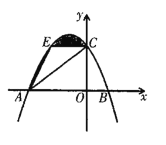
(1)求点A、B、C的坐标;
(2)若点E与点C关于抛物线的对称轴对称,求梯形AOCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com