
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
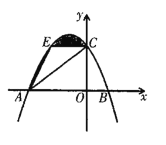
(1)求点A、B、C的坐标;
(2)若点E与点C关于抛物线的对称轴对称,求梯形AOCE的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
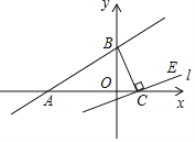
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0)、B(0,6),过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.
(1)求一次函数y=kx+b(k≠0)的解析式;
(2)求直线l的解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校院墙上部是由![]() 段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔
段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔![]() ,加设一根不锈钢支柱,防护栏的最高点据护栏底部
,加设一根不锈钢支柱,防护栏的最高点据护栏底部![]() (如图),则这条护栏要不锈钢支柱总长度至少为( )
(如图),则这条护栏要不锈钢支柱总长度至少为( )

A. 50m B. 100m C. 120m D. 160m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B.C两点后就停止移动,回答下列问题:
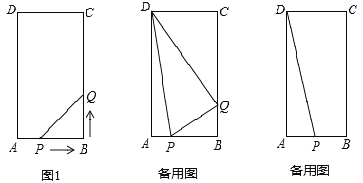
(1)运动开始后第几秒时, △PBQ的面积等于8![]() ?
?
(2)当t=![]() 时,试判断△DPQ的形状。
时,试判断△DPQ的形状。
(3)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com