
【题目】我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设![]() 为三角形三边,
为三角形三边,![]() 为面积,则
为面积,则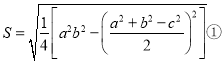 ,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设
,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设![]() (周长的一半),则
(周长的一半),则![]()
(1)尝试验证.这两个公式在表面上形式很不一致,请你用以![]() 为三边构成的三角形,分别验证它们的面积值;
为三边构成的三角形,分别验证它们的面积值;
(2)问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从![]() 或者
或者![]() );
);
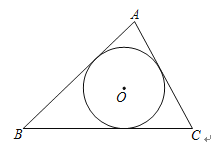
(3)问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图,![]() 的内切圆半径为
的内切圆半径为![]() ,三角形三边长为
,三角形三边长为![]() ,仍记
,仍记![]() ,
,![]() 为三角形面积,则
为三角形面积,则![]() .
.
科目:初中数学 来源: 题型:
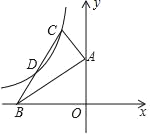
【题目】如图坐标系中,Rt△BAC的直角顶点A在y轴上,顶点B在x轴上,且OA=4,OB=6,双曲线y=![]() 经过点和斜边BC的中点D,则k=_____.
经过点和斜边BC的中点D,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,对称轴是直线
的图象如图所示,对称轴是直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤方程
;⑤方程![]() 有一正一负两个实数解.其中结论正确的个数为( )
有一正一负两个实数解.其中结论正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
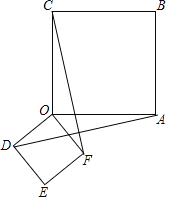
【题目】如图,四边形![]() 与四边形
与四边形![]() 都是正方形.
都是正方形.
(1)当正方形![]() 绕点
绕点![]() 在平面内旋转时,
在平面内旋转时,![]() 与
与![]() 有怎样的数量和位置关系?”并证明你的结论:
有怎样的数量和位置关系?”并证明你的结论:
(2)若![]() ,正方形
,正方形![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 转到直线
转到直线![]() 上时,
上时,![]() 恰好是
恰好是![]() ,试问:当点
,试问:当点![]() 转到直线
转到直线![]() 或直线
或直线![]() 上时,求
上时,求![]() 的长(本小题画出图形并写出结论,不必写出过程)
的长(本小题画出图形并写出结论,不必写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0)、B(0,6),过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.
(1)求一次函数y=kx+b(k≠0)的解析式;
(2)求直线l的解析式;
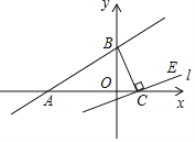
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B.C两点后就停止移动,回答下列问题:
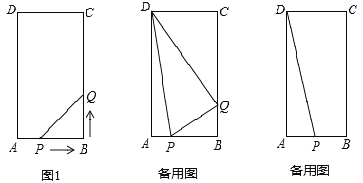
(1)运动开始后第几秒时, △PBQ的面积等于8![]() ?
?
(2)当t=![]() 时,试判断△DPQ的形状。
时,试判断△DPQ的形状。
(3)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com