
【题目】如图,四边形![]() 与四边形
与四边形![]() 都是正方形.
都是正方形.
(1)当正方形![]() 绕点
绕点![]() 在平面内旋转时,
在平面内旋转时,![]() 与
与![]() 有怎样的数量和位置关系?”并证明你的结论:
有怎样的数量和位置关系?”并证明你的结论:
(2)若![]() ,正方形
,正方形![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 转到直线
转到直线![]() 上时,
上时,![]() 恰好是
恰好是![]() ,试问:当点
,试问:当点![]() 转到直线
转到直线![]() 或直线
或直线![]() 上时,求
上时,求![]() 的长(本小题画出图形并写出结论,不必写出过程)
的长(本小题画出图形并写出结论,不必写出过程)
【答案】(1)AD=CF且AD⊥CF;(2)![]() +1或
+1或![]() -1或2.
-1或2.
【解析】
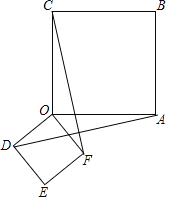
(1)结论:AD=CF且AD⊥CF.如图1中,设CF交OA于K,交AD于J.证明△AOD≌△COF(SAS)即可解决问题.
(2)根据条件首先求出正方形ODEF的边长,分四种情形分别求解即可解决问题.
(1)结论:AD=CF且AD⊥CF.
理由:如图1中,设CF交OA于K,交AD于J.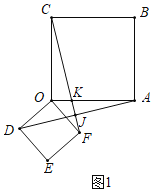
∵四边形OABC与四边形ODEF都是正方形,
∴OA=OC,OD=OF,∠AOC=∠DOF=90°,
∴∠AOD=∠COF,
∴△AOD≌△COF(SAS),
∴AD=CF,∠OCF=∠OAD,
∵∠OCK+∠OKC=90°,∠OKC=∠AKJ,
∴∠AKJ+∠KAJ=90°,
∴∠AJK=90°
∴AD⊥CF.
(2)如图2中,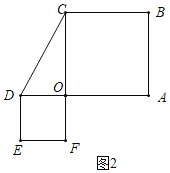
由题意:在Rt△COD中,∠COD=90°,OC=OA=![]() ,∠OCD=30°,
,∠OCD=30°,
∴OD=OCtan30°=![]() =1,
=1,
此时AD=1+![]()
如图3中,当点D在CO的延长线上时,AD=![]() =2.
=2.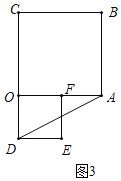
如图4中,当点D在线段OA上时,AD=![]() -1,
-1,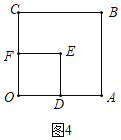
如图5中,当点D在线段OC上时,AD=![]() =2,
=2,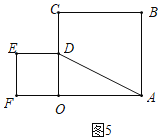
综上所述,满足条件的AD的值为![]() +1或
+1或![]() -1或2.
-1或2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面6.4米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,
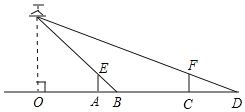
求:(1)小方在A处时的影子AB的长;(2)小方行走的路程AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg.
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设![]() 为三角形三边,
为三角形三边,![]() 为面积,则
为面积,则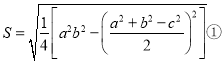 ,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设
,这是中国古代数学的瑰宝之一.而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设![]() (周长的一半),则
(周长的一半),则![]()
(1)尝试验证.这两个公式在表面上形式很不一致,请你用以![]() 为三边构成的三角形,分别验证它们的面积值;
为三边构成的三角形,分别验证它们的面积值;
(2)问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从![]() 或者
或者![]() );
);
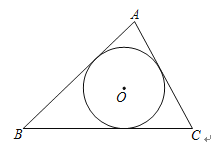
(3)问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图,![]() 的内切圆半径为
的内切圆半径为![]() ,三角形三边长为
,三角形三边长为![]() ,仍记
,仍记![]() ,
,![]() 为三角形面积,则
为三角形面积,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形满足下列条件,那么它们一定相似的是( )
A. 有一个角相等的两个等腰三角形
B. 有一个角相等的两个直角三角形
C. 有一个角是![]() 的两个等腰三角形
的两个等腰三角形
D. 有一组角是对顶角的两个三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)(2x-1)2-16=0;
(2)6x2-5x-1=0;
(3)25(x+1)2=9(x-2)2 ;
(4)2y(y-1)+3=(y+1)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com