
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 与边
与边![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 于点
于点![]() .
.
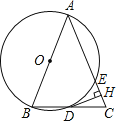
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证:![]() 为
为![]() 的中点;
的中点;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() 与
与![]() 相切,理由见解析;(2)详见解析;(3)
相切,理由见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)连结![]() 、
、![]() ,如图1,先利用AB是圆的直径得到
,如图1,先利用AB是圆的直径得到![]() ,再根据等腰三角形的性质得
,再根据等腰三角形的性质得![]() ,然后利用三角形中位线定理可得
,然后利用三角形中位线定理可得![]() ,而
,而![]() ,进一步即可证得结论;
,进一步即可证得结论;
(2)连结![]() ,如图2,根据圆内接四边形的性质和等腰三角形的性质可得
,如图2,根据圆内接四边形的性质和等腰三角形的性质可得![]() ,从而DE=DC,然后根据等腰三角形三线合一的性质即可证得结论;
,从而DE=DC,然后根据等腰三角形三线合一的性质即可证得结论;
(3)易得![]() ,利用余弦的定义,分别在
,利用余弦的定义,分别在![]() 和
和![]() 中计算出AC与CH的长,则CE即可求出,然后计算
中计算出AC与CH的长,则CE即可求出,然后计算![]() 即可得到
即可得到![]() 的长.
的长.
解:(1)![]() 与
与![]() 相切.理由如下:
相切.理由如下:
连结![]() 、
、![]() ,如图1,∵
,如图1,∵![]() 为直径,∴
为直径,∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
而![]() ,∴
,∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 为
为![]() 的切线;
的切线;
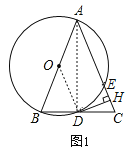
(2)证明:连结![]() ,如图2,
,如图2,
∵四边形![]() 为
为![]() 的内接四边形,∴
的内接四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴DE=DC.
,∴DE=DC.
∵![]() ,∴
,∴![]() ,即
,即![]() 为
为![]() 的中点;
的中点;
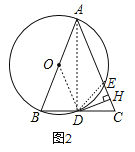
(3)解:如图2,在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的周长是48cm, AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
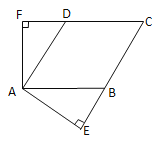
(1)求∠C的度数;
(2)已知DF的长是关于x的方程x2-5x-a=0的一个根,求该方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
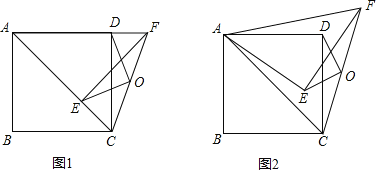
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
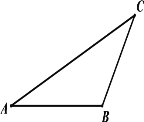
【题目】(1)在△ABC中,∠BAC=60°,BC=4![]() ,则△ABC面积的最大值是 .
,则△ABC面积的最大值是 .
(2)已知:△ABC,用无刻度的直尺和圆规求作△DBC,使∠BDC+∠A=180°,且BD=DC.(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注,作出一个符合题意的三角形即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
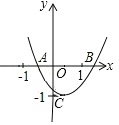
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() .则由抛物线的特征写出如下结论:①
.则由抛物线的特征写出如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的个数是()
.其中正确的个数是()
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,对称轴是直线
的图象如图所示,对称轴是直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤方程
;⑤方程![]() 有一正一负两个实数解.其中结论正确的个数为( )
有一正一负两个实数解.其中结论正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
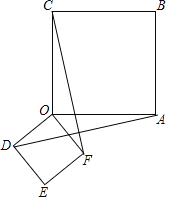
【题目】如图,四边形![]() 与四边形
与四边形![]() 都是正方形.
都是正方形.
(1)当正方形![]() 绕点
绕点![]() 在平面内旋转时,
在平面内旋转时,![]() 与
与![]() 有怎样的数量和位置关系?”并证明你的结论:
有怎样的数量和位置关系?”并证明你的结论:
(2)若![]() ,正方形
,正方形![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 转到直线
转到直线![]() 上时,
上时,![]() 恰好是
恰好是![]() ,试问:当点
,试问:当点![]() 转到直线
转到直线![]() 或直线
或直线![]() 上时,求
上时,求![]() 的长(本小题画出图形并写出结论,不必写出过程)
的长(本小题画出图形并写出结论,不必写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com