
【题目】(1)在△ABC中,∠BAC=60°,BC=4![]() ,则△ABC面积的最大值是 .
,则△ABC面积的最大值是 .
(2)已知:△ABC,用无刻度的直尺和圆规求作△DBC,使∠BDC+∠A=180°,且BD=DC.(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注,作出一个符合题意的三角形即可)
【答案】(1)12![]() ;(2)如图所示见解析.
;(2)如图所示见解析.
【解析】
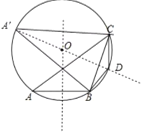
(1)作AB、BC的垂直平分线,它们相交于点O,再以点O为圆心,OA为半径作圆得到△ABC的外接圆,利用三角形面积公式得到当点A到BC的距离最大时,△ABC面积的最大,此时点A在优弧BC的中点,利用圆周角定理可判断△A′BC为等边三角形,然后利用等边三角形的面积的计算方法可得到△ABC面积的最大值;
(2)BC的垂直平分线交BC弧于D,根据垂径定理得到弧BD=弧CD,根据圆周角定理得到∠BDC+∠A=180°,从而可判断△DBC满足条件.
解:(1)作△ABC的外接圆⊙O,
当点A到BC的距离最大时,△ABC面积的最大,此时点A在BC的垂直平分线上,
如图,点A在A′时△ABC的面积最大,
∵∠BA′C=∠BAC=60°,
A′B=A′C,
∴△A′BC为等边三角形,
∴△ABC面积的最大值=![]() ×(4
×(4![]() )2=12
)2=12![]()
故答案为12![]() ,
,
(2)如图,△DBC为所作.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 点以
点以![]() 的速度移动.
的速度移动.
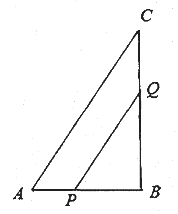
(1)如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,几秒钟后,
同时出发,几秒钟后,![]() 的面积等于
的面积等于![]() ?
?
(2)在(1)中,![]() 的面积能否等于
的面积能否等于![]() 面积的一半?说明理由;
面积的一半?说明理由;
(3)几秒后,点![]() ,点
,点![]() 相距
相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面6.4米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,
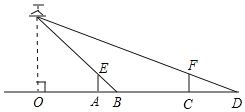
求:(1)小方在A处时的影子AB的长;(2)小方行走的路程AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 、点
、点![]() 在直线
在直线![]() 上,反比例函数
上,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() .
.
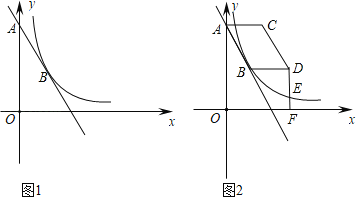
(1)求![]() 和
和![]() 的值;
的值;
(2)将线段![]() 向右平移
向右平移![]() 个单位长度(
个单位长度(![]() ),得到对应线段
),得到对应线段![]() ,连接
,连接![]() 、
、![]() .
.
①如图2,当![]() 时,过
时,过![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,求
,求![]() 的值;
的值;
②在线段![]() 运动过程中,连接
运动过程中,连接![]() ,若
,若![]() 是以
是以![]() 为腰的等腰三形,求所有满足条件的
为腰的等腰三形,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, AB=AC=10,线段BC在![]() 轴上,BC=12,点B的坐标为(-3,0),线段AB交
轴上,BC=12,点B的坐标为(-3,0),线段AB交![]() 轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿
轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿![]() 轴向右运动,设运动的时间为
轴向右运动,设运动的时间为![]() 秒.
秒.
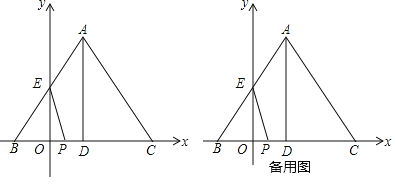
(1)当△BPE是等腰三角形时,求![]() 的值;
的值;
(2)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切时,求![]() 的值和此时点C的坐标.
的值和此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg.
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com