
【题目】用适当的方法解下列方程:
(1)(2x-1)2-16=0;
(2)6x2-5x-1=0;
(3)25(x+1)2=9(x-2)2 ;
(4)2y(y-1)+3=(y+1)2.
【答案】(1)x=![]() ,x=-
,x=-![]() ; (2)x=1,x=-
; (2)x=1,x=-![]() ;(3)x=-
;(3)x=-![]() , x=
, x=![]() ; (4)y=2+
; (4)y=2+![]() , y=2-
, y=2-![]() .
.
【解析】
(1)利用因式分解法解方程;(2)利用因式分解法解方程;(3)利用直接开平方法解方程;(4)先把原方程化为标准一元二次方程,然后再用公式解方程.
解:(1)(2x-1-4)(2x-1+4)=0,
2x-1-4=0或2x-1+4=0,
所以x1=![]() ,x=-
,x=-![]() ;
;
(2)(6x+1)(x-1)=0,
6x+1=0或x-1=0,
所以x1=-![]() ,x2=1;
,x2=1;
(3)25(x+1)2=9(x-2)2 ,
5(x+1)=±3(x-2),
所以x1=-![]() , x2=
, x2=![]() ;
;
(4)由原方程,得
2y2-2y+3=y2+2y+1,即y2-4y+2=0,
∴a=1,b=-4,c=2.
b2-4ac=(-4)2-4×1×2=8>0.
![]()
y1=2+![]() , y2=2-
, y2=2-![]() .
.


科目:初中数学 来源: 题型:
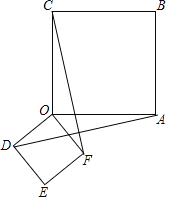
【题目】如图,四边形![]() 与四边形
与四边形![]() 都是正方形.
都是正方形.
(1)当正方形![]() 绕点
绕点![]() 在平面内旋转时,
在平面内旋转时,![]() 与
与![]() 有怎样的数量和位置关系?”并证明你的结论:
有怎样的数量和位置关系?”并证明你的结论:
(2)若![]() ,正方形
,正方形![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 转到直线
转到直线![]() 上时,
上时,![]() 恰好是
恰好是![]() ,试问:当点
,试问:当点![]() 转到直线
转到直线![]() 或直线
或直线![]() 上时,求
上时,求![]() 的长(本小题画出图形并写出结论,不必写出过程)
的长(本小题画出图形并写出结论,不必写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校院墙上部是由![]() 段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔
段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔![]() ,加设一根不锈钢支柱,防护栏的最高点据护栏底部
,加设一根不锈钢支柱,防护栏的最高点据护栏底部![]() (如图),则这条护栏要不锈钢支柱总长度至少为( )
(如图),则这条护栏要不锈钢支柱总长度至少为( )

A. 50m B. 100m C. 120m D. 160m
查看答案和解析>>
科目:初中数学 来源: 题型:
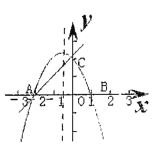
【题目】已知关于x的二次函数y =-x2+(k-2)x+k+1.
(1)求证:该函数的图象与x轴一定有两个交点;
(2)当k =1时,设该函数的图象与x轴的交点为A、B(A在B的左侧),与y轴的交点为C,点P为其图象的对称轴上一动点,是否存在点P,使BP+CP最小,若存在,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B.C两点后就停止移动,回答下列问题:
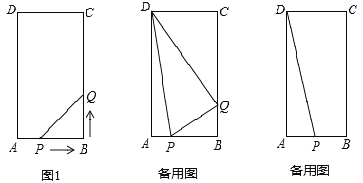
(1)运动开始后第几秒时, △PBQ的面积等于8![]() ?
?
(2)当t=![]() 时,试判断△DPQ的形状。
时,试判断△DPQ的形状。
(3)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
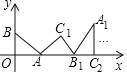
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com