计算：（1）（4分）20﹣（﹣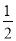
）+（﹣12）+
；
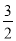（2）（4分）﹣22 + 3 ×（﹣1）2015 +（﹣4）×5；
（3）（6分）先化简，再求值：（﹣x2 + 3x+ 4）﹣（3x+ 4﹣2x2），其中x=2；
（4）（4分）解方程：3x+2（5-x）=5．
（1）10；（2）-27；（3） x2 ；4；（4）3．
【解析】
试题分析：（1）首先去括号，然后应用加法交换律、结合律凑整，得到结果；
（2）根据有理数的混合运算法则，先计算乘方，再计算加减；
（3）先化简代数式，得原式= x2，然后把x=2代入求值；
（4）根据解一元一次方程的步骤逐步进行变形，得到x的值．
试题解析：【解析】
（1） 20﹣（﹣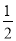
）+（﹣12）+
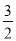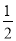=20++（﹣12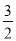）+=[20+（﹣12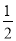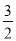）]+（+） =8+2 =10；
（2）﹣22+ 3×（﹣1）2015+（﹣4）×5=﹣4+ 3×（﹣1）+（﹣20） =﹣4+（﹣3）+（﹣20） =﹣27；
（3）（﹣x2 +3x+ 4）﹣（3x+4﹣2x2） =﹣x2 + 3x+ 4﹣3x﹣4+2x2 =（﹣x2+2x2）+（3x﹣3x） + （4﹣4 ）= x2+0+0 = x2 ；
当x = 2时，上式 = 22= 4；
（4）【解析】
去括号得：3x-10+2x=5，
移项，得：3x + 2x = 5 + 10 ，
合并同类项，得：5x = 15，
方程两边同除以5，得：x = 3．
考点：有理数的运算；代数式的化简求值；一元一次方程的解法．
科目：初中数学 来源： 题型：
已知二次函数y=x2-4x+3.
(1)用配方法求其函数图象的顶点C的坐标，并描述该函数的函数值随自变量的增减而增减的情况；
(2)求函数图象与x轴的交点A，B的坐标，及△ABC的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体，抽屉底面周长为180 cm，高为20 cm.请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？(材质及其厚度等暂忽略不计)
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省七年级上学期期末考试数学试卷（解析版） 题型：解答题
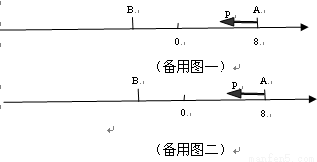
（9分）如图，已知数轴上点A表示的数为8，B是数轴上的一点，AB=12，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
（1）写出数轴上点B表示的数 ，经t秒后点P走过的路程为 （用含t的代数式表示）；（2分）
（2）若在动点P运动的同时另一动点Q从点B也出发，并以每秒4个单位长度的速度沿数轴向左匀速运动，问经多长时间点P就能追上点Q？（4分）
（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长．（3分）
查看答案和解析>>
科目：初中数学 来源： 题型：
便民商店经营一种商品，在销售过程中，发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2x2+80x+750，由于某种原因，售价只能满足15≤x≤22，那么一周可获得的最大利润是 元.
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省福安市八年级上学期期末考试数学试卷（解析版） 题型：解答题
（本题满分6分）一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三方面为选手打分，各项成绩均按百分制，进入决赛的两名选手的单项成绩如下表所示：
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
演讲内容 | 演讲能力 | 演讲效果 | |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
（1）如果认为这三方面的成绩同等重要，从他们的成绩看，谁将胜出？
（2）如果按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例来计算甲、乙的平均成绩，那么谁将胜出？
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，OB是∠AOC的角平分线，OD是∠COE的角平分线.如果∠AOB=40°，∠COE=60°，则
∠BOD的度数为( )
A.50° B.60° C.65° D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象的交点位于( )