科目：初中数学 来源： 题型：
确定一次函数的解析式
| 常用方法 |
|
| 步骤 | ①设函数 |
| 常见类型 | ①已知两点坐标确定解析式；②已知两对函数对应值确定解析式；③通过平移规律确定函数解析式. |
【易错提示】在已知自变量和函数的取值范围确定函数解析式时，要注意函数性质的影响，防止漏解.
考点5 一次函数与方程、不等式的关系
| 一次函数与一次方程 | 一元一次方程kx+b=0的根就是一次函数y=kx+b(k、b是常数,k≠0)的图象与 |
| 一次函数与一元一次不等式 | 一元一次不等式kx+b＞0(或kx+b＜0)(k≠0)的解集可以看作一次函数y=kx+b取 |
| 一次函数与方程组 | 两直线的交点坐标是两个一次函数解析式y=k1x+b1和y=k2x+b2所组成的关于x、y的方程组 |
查看答案和解析>>
科目：初中数学 来源： 题型：
“一根弹簧原长10 cm，在弹性限度内最多可挂质量为5 kg的物体，挂上物体后弹簧伸长的长度与所挂物体的质量成正比，
，则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染，被污染的部分是确定函数关系式的一个条件，你认为该条件可以是： (只需写出1个).
查看答案和解析>>
科目：初中数学 来源： 题型：
将油箱注满k升油后，轿车可行驶的总路程s(单位：千米)与平均耗油量a(单位：升/千米)之间是反比例函数关系s=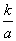
(k是常数，k≠0).已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式(关系式).
(2)当平均耗油量为0.08升/千米时，该轿车可以行驶多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，抛物线y=a(x-1)2+4与x轴交于点A，B，与y轴交于点C.过点C作CD∥x轴交抛物线的对
称轴于点D，连接BD.已知点A的坐标为(-1,0).
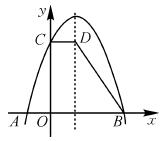
(1)求抛物线的解析式；
(2)求梯形COBD的面积.
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省七年级上学期期末考试数学试卷（解析版） 题型：解答题
计算：（1）（4分）20﹣（﹣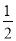
）+（﹣12）+
；
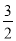（2）（4分）﹣22 + 3 ×（﹣1）2015 +（﹣4）×5；
（3）（6分）先化简，再求值：（﹣x2 + 3x+ 4）﹣（3x+ 4﹣2x2），其中x=2；
（4）（4分）解方程：3x+2（5-x）=5．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象的交点位于( )
；②列方程(组)；③解方程（组)确定待定系数；④确定解析式.
轴交点的
坐标.
值(或
值)时自变量x的取值范围.
的解.
于A，B两点，P是x轴上任意一点，则△ABP的面积等于 .
图象的一个交点坐标为(-1,2)，则另一个交点的坐标为 .