
(9分)如图,已知数轴上点A表示的数为8,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ,经t秒后点P走过的路程为 (用含t的代数式表示);(2分)
(2)若在动点P运动的同时另一动点Q从点B也出发,并以每秒4个单位长度的速度沿数轴向左匀速运动,问经多长时间点P就能追上点Q?(4分)

(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.(3分)
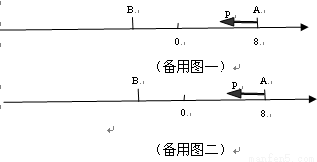
(1)- 4;6t;(2)6秒;(3)MN的长度不变,MN=6.
【解析】
试题分析:(1)点B与原点的距离为12-8=4,据此得到点B所对应的数轴上的数,根据路程=速度×时间得到点P运动的路程;
(2)设经t秒后P点追上Q点,根据点P和点Q的路程之差为12列方程,解得t的值;
(3)分两种情形分析:①点P在线段AB上时,MN=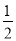 AB;②点P在B点左侧时,MN=
AB;②点P在B点左侧时,MN=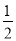 AB,据此即可得到MN的长度.
AB,据此即可得到MN的长度.
试题解析:【解析】
(1)点B表示的数为- 4,经t秒后点P走过的路程为6t;
故答案为:- 4;6t;
(2)设经t秒后P点追上Q点,根据题意可列方程:6t-4t =12 ,解得:t=6 ,
答:经过6秒后P点能追上Q点。
(3)不论P运动到哪里,线段MN都等于6.
分两种情形分析:
①点P在线段AB上时,
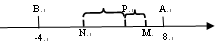
MN=PM+PN=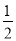 PA+
PA+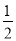 PB =
PB =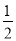 (PA+PB)=
(PA+PB)=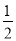 AB=
AB=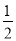 ×12=6;
×12=6;
②点P在B点左侧时,
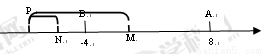
MN=PM-PN=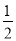 PA-
PA-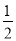 PB=
PB=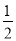 (PA-PB)=
(PA-PB)=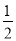 AB=
AB=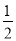 ×12=6,
×12=6,
综上可知,不论P运动到哪里,线段MN的长度都不变,都等于6.
考点:线段的和差;线段的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
将油箱注满k升油后,轿车可行驶的总路程s(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系s=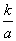 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式(关系式).
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
某商店经营一种小商品,进价为每件20元,据市场分析,在一个月内,售价定为25元时,可卖出105件,而售价每上涨1元,就少卖5件.
(1)当售价定为每件30元时,一个月可获利多少元?
(2)当售价定为每件多少元时,一个月的获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个)…30405060…销售量y(万个)…5432…同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用学过的一次函数、反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式;
(2)求得该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得 利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:解答题
计算:(1)(4分)20﹣(﹣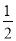 )+(﹣12)+
)+(﹣12)+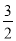 ;
;
(2)(4分)﹣22 + 3 ×(﹣1)2015 +(﹣4)×5;
(3)(6分)先化简,再求值:(﹣x2 + 3x+ 4)﹣(3x+ 4﹣2x2),其中x=2;
(4)(4分)解方程:3x+2(5-x)=5.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级下学期期始考试数学试卷(解析版) 题型:填空题
四张完全相同的卡片上分别画有平行四边形、等边三角形、线段、圆,背面朝上洗匀后,放在桌面上,从中随机抽取两张,抽的两张卡片上的图形都是中心对称图形的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com