练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知二次函数y=x2-4x+3.

    (1)用配方法求其函数图象的顶点C的坐标，并描述该函数的函数值随自变量的增减而增减的情况；

    (2)求函数图象与x轴的交点A，B的坐标，及△ABC的面积.


    (1)y=x2-4x+3=(x-2)2-1.

    ∴其函数的顶点C的坐标为(2，-1)，

    ∴当x<2时，y随x的增大而减小；

    当x>2时，y随x的增大而增大.

    (2)令y=0，则x2-4x+3=0,解得x1=1,x2=3.

    ∴当点A在点B左侧时，A(1，0)，B(3，0)；

    当点A在点B右侧时，A(3，0)，B(1，0).

    ∴AB=|1-3|=2.

    过点C作CD⊥x轴于D，则

    △ABC的面积=AB·CD=×2×1=1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    “一根弹簧原长10 cm，在弹性限度内最多可挂质量为5 kg的物体，挂上物体后弹簧伸长的长度与所挂物体的质量成正比，，则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染，被污染的部分是确定函数关系式的一个条件，你认为该条件可以是：                      (只需写出1个).

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E、F两点.若E是AB的中点，S△BEF=2，则k的值为          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，抛物线y=a(x-1)2+4与x轴交于点A，B，与y轴交于点C.过点C作CD∥x轴交抛物线的对称轴于点D，连接BD.已知点A的坐标为(-1,0).

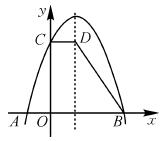
    (1)求抛物线的解析式；

    (2)求梯形COBD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点，那么m的值为(     )

      A.0                 B.0或2                 C.2或-2               D.0，2或-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


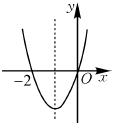
    已知二次函数y＝ax2+bx+c(a≠0)的图象如图所示，则下列说法：①c＝0；②该抛物线的对称轴是直线x＝-1；③当x＝1时，y＝2a；④am2+bm+a＞0(m≠-1).其中正确的个数是(     )

      A.1               B.2            C.3               D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商店经营一种小商品，进价为每件20元，据市场分析，在一个月内，售价定为25元时，可卖出105件，而售价每上涨1元，就少卖5件.

    (1)当售价定为每件30元时，一个月可获利多少元？

    (2)当售价定为每件多少元时，一个月的获利最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年福建省七年级上学期期末考试数学试卷（解析版） 题型：解答题

    计算：（1）（4分）20﹣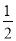（﹣）+（﹣12）+；

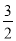    （2）（4分）﹣22 + 3 ×（﹣1）2015 +（﹣4）×5；

    （3）（6分）先化简，再求值：（﹣x2 + 3x+ 4）﹣（3x+ 4﹣2x2），其中x=2；

    （4）（4分）解方程：3x+2（5-x）=5．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年福建省福安市八年级上学期期末考试数学试卷（解析版） 题型：填空题

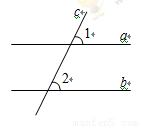
    如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2= °．

    查看答案和解析>>

    同步练习册答案