
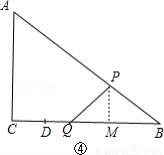
(本题满分10分)如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C出发,以2cm/s的速度沿C→A→B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5 s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当 时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.

(1)CD = ,  ;
;
(2)当点P在边AB上时,t为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时t的值.
(1)CD=2,a=10.8;(2)4.25秒或6秒;(3)5秒或 秒
秒
【解析】
试题分析:(1)当点P运动到点A时,△BPQ的面积为18,
∴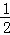 •6•BD=18,解得BD=6,
•6•BD=18,解得BD=6,
∴CD=BC﹣BD=2,
当t=5s时,AP=2×5﹣6=4,点Q在D点,点P在AB上如图①,作PH⊥BC于H,
在Rt△ABC中,AC=6,BC=8,
∴AB=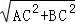 =10,
=10,
∵PH∥AC,
∴△BPH∽△BAC,
∴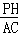 =
=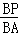 ,即
,即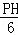 =
=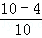 ,解得PH=
,解得PH=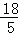 ,
,
∴S△PBQ=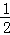 ×6×
×6×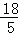 =
=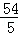 ,
,
即a=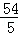 ;
;
故答案为:2,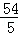 ;
;
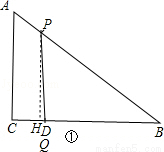
(2)点P在边AB上,
当3<t≤5,点Q在D点,BP=16﹣2t,
若PD⊥BC,△BPQ∽△BAC,
∴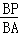 =
=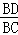 ,即
,即 =
=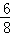 ,解得t=
,解得t= ;
;
当5<t≤8,DQ=t﹣5,则BQ=8﹣2﹣(t﹣5)=11﹣t,BP=16﹣2t,
当∠PQB=90°时,△BPQ∽△BAC,如图②,
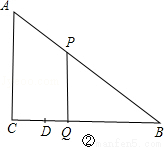
∵△BPQ∽△BAC,
∴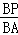 =
=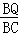 ,即
,即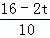 =
=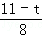 ,解得t=3,不合题意舍去;
,解得t=3,不合题意舍去;
当∠BPQ=90°时,△BPQ∽△BAC,如图③,
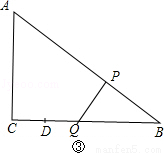
∵△BPQ∽△BCA,
∴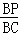 =
=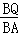 ,即
,即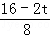 =
=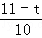 ,解得t=6,
,解得t=6,
综上所述,当t为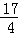 或6时,△BPQ与△ABC为相似;
或6时,△BPQ与△ABC为相似;
(3)PB=16﹣2t,BQ=11﹣t,
当BP=BQ,则16﹣2t=11﹣t,解得t=5;
当PB=PQ,作PM⊥BC于M,如图④,则BM= BQ=
BQ= (11﹣t),
(11﹣t),
∵PM∥AC,
∴△BPM∽△BAC,
∴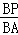 =
= ,即
,即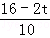 =
=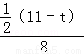 ,解得t=
,解得t=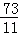 ,
,
综上所述,当△BPQ是以BP为腰的等腰三角形时t的值为5或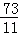 .
.
考点:1.相似形综合题;2.动点问题的函数图象;3.勾股定理的应用


科目:初中数学 来源:2014-2015学年江苏省无锡市新区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市新区七年级上学期期中考试数学试卷(解析版) 题型:选择题
在下列各数中,结果是负数的是( )
A.-(-3) B.-(-3)3 C.(-3)2 D.-|-3|
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区八年级上学期期中考试数学试卷(解析版) 题型:填空题
16的平方根为________ ;(-4)3的立方根是____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区八年级上学期期中考试数学试卷(解析版) 题型:选择题
如下图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )

A.线段CD的中点
B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点
D.CD与∠AOB的平分线的交点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在平面直角坐标系中,△AOB的顶点坐标分别为A(2,1)、O(0,0)、B(1,-2).

(1)P(a,b)是△AOB的边AB上一点,△AOB经平移后点P的对应点为P2(a-3, b+1),请画出上述平移后的△A1O1B1,并写出点A1的坐标;
(2)以点O为位似中心,在y轴的右侧画出△AOB的一个位似△A2OB2,使它与△AOB的相似比为2:1,并分别写出点A、P的对应点A2、P2的坐标;
(3)判断△A2OB2与△A1O1B1能否是关于某一点Q为位似中心的位似图形,若是,请在图10中标出位似中心Q,并写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 °

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题7分)世博会某国国家馆模型的平面图如图所示,其外框是一个大正方形,中间四个大小相同的小正方形(阴影部分)是支撑展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米.

(1)若设展厅的正方形边长为x米,用含x的代数
式表示核心筒的正方形边长为 米.
(2)若设核心筒的正方形边长为y米,求该模型的平面图外框大正方形的周长及每个休息厅的图形周长.(用含y的代数式表示)
(3)若设核心筒的正方形边长为2米,求该国家展厅(除四根核心筒)的占地面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市崇安区九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;② ;③AC·BE=12;④3BF=4AC.其中正确结论的个数有( )
;③AC·BE=12;④3BF=4AC.其中正确结论的个数有( )
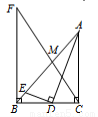
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com