
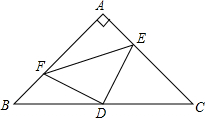
 已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.
已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.分析 (1)连接AD,证明△BFD≌△AED,根据全等三角形的性质即可得出DE=DF;
(2)根据△DAE≌△DBF,得到四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC,于是得到结论.
解答 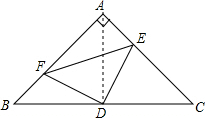 证明:(1)连接AD,
证明:(1)连接AD,
∵Rt△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵AB=AC,DB=CD,
∴∠DAE=∠BAD=45°,
∴∠BAD=∠B=45°,
∴AD=BD,∠ADB=90°,
在△DAE和△DBF中,
$\left\{\begin{array}{l}{AE=BF}\\{∠DAE=∠B=45°}\\{AD=BD}\end{array}\right.$,
∴△DAE≌△DBF(SAS),
∴DE=DF;
(2)∵△DAE≌△DBF,
∴四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC,
∵BC=8,
∴AD=$\frac{1}{2}$BC=4,
∴四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×\frac{1}{2}×8×4$=8.
点评 本题主要考查了全等三角形的判定和等腰三角形的判定.考查了学生综合运用数学知识的能力,连接AD,构造全等三角形是解决问题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
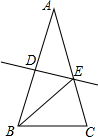 如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com