
【题目】如图 1,长方形 ABCD 中,AB=3cm,BC=6cm,P 为矩形 ABCD 上的动点,动点 P 从 A 出发,沿着 A-B-C-D 运动到 D 点停止,速度为 1cm/s,设点 P 运动时间为 x 秒,△APD 的面积为 ycm.
(1)填空:①当 x=6 时,对应 y 的值为________;9≤x<12 时,y 与 x 之间的关系式为_____;
(2)当 y=3 时,求 x 的值;
(3)当 P 在线段 BC 上运动时,是否存在点 P 使得△APD 的周长最小?若存在,求出此时∠APD 的度数;若不存在,请说明理由.

图1
【答案】 9 y=-3x+36
【解析】(1)利用三角形面积求法S△APD=![]() 即可得出答案;当9<x≤12时,点P运动到CD边上,S△APD=
即可得出答案;当9<x≤12时,点P运动到CD边上,S△APD=![]() 得出y与x的函数关系式即可;
得出y与x的函数关系式即可;
(2)分别求出点P在AB、BC、CD上y与x的函数关系式,利用y=3,求出x的值即可;
(3)利用轴对称求最短路线的方法得出P点位置,进而利用全等三角形的性质求出答案.
(1)9;y=-3x+36;
(2)当 P 从 A-B 运动时,y=3x;当 P 从 B-C 运动时,y=9;当 P 从 C-D 运动时,y=-3x+36;令 y=3,则 3x=3 或-3x+36=3,解得 x=1 或 11.
(3)存在.理由:如图,延长 DC,使得 DC=D’C,连接 AD’,交 BC 于点 P,则 P 为所求,

且△PCD≌△PCD’,
∴PD=PD’,∠PCD=∠PCD’ 因为四边形 ABCD 是长方形
∴AB=CD,∠B=∠PCD=90°
∴AB=CD’,∠PCD’=90°
在△ABP 与△D’CP 中,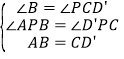
∴△ABP≌△D’CP(AAS)
∴BP PC![]() BC3,
BC3,
∵AB=DC=3,
∴AB=BP,PC=CD,
∴∠APB=∠BAP=45°,∠DPC=∠DPC=45°,
∵∠APB+∠APD+∠CPD=180°,
∴∠APD=90°.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
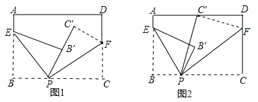
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( ) 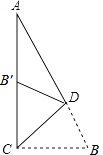
A.40°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P. 
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) 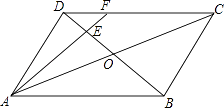
A.1:4
B.1:3
C.1:2
D.1:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 度;
(2)判断△BEF的形状为 ;
(3)若∠BFC=90°,说明AE∥BF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com