
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
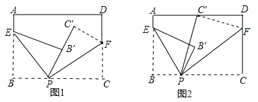
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
【答案】(1)90°;(2)85°
【解析】分析:(1)由对称性得到两对角相等,而这两对角之和为180°,利用等量代换及等式的性质即可求出折痕的夹角∠EPF的度数;
(2)由对称性得到两对角相等,根据题意得到这两对角之和为190°,利用等量代换及等式的性质即可求出∠EPF的度数.
详解:(1)由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF.
∵∠BPE+∠B′PE+∠CPF+∠C′PF=180°,∴∠EPF=∠B′PE+∠C′PF=![]() ×180°=90°;
×180°=90°;
(2)由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF.
∵∠BPE+∠B′PE+∠CPF+∠C′PF=180°+10°=190°,∴∠BPE+∠CPF=95°,∴∠FPE=85°.


科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( )
上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( ) 
A.8﹣2 ![]()
B.8+2 ![]()
C.3
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
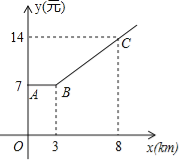
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,长方形 ABCD 中,AB=3cm,BC=6cm,P 为矩形 ABCD 上的动点,动点 P 从 A 出发,沿着 A-B-C-D 运动到 D 点停止,速度为 1cm/s,设点 P 运动时间为 x 秒,△APD 的面积为 ycm.
(1)填空:①当 x=6 时,对应 y 的值为________;9≤x<12 时,y 与 x 之间的关系式为_____;
(2)当 y=3 时,求 x 的值;
(3)当 P 在线段 BC 上运动时,是否存在点 P 使得△APD 的周长最小?若存在,求出此时∠APD 的度数;若不存在,请说明理由.

图1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有3个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是________.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com