
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
【答案】 ![]() 60°
60°
【解析】试题分析:请回答:由图2及其做法可得:EF=CD=3,CF=DE,所以BC+DE=BF,在Rt△BEF中由勾股定理可得BF=![]() ;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
试题解析:解:BC+DE的值为![]() . 2分
. 2分
解决问题:
连接AE,CE,如图.

∵四边形ABCD是平行四边形,
∴AB //DC.
∵四边形ABEF是矩形,
∴AB //FE,BF=AE.
∴DC //FE.
∴四边形DCEF是平行四边形. 3分
∴CE //DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形. 4分
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°. 5分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F.
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )

A. (1)(5)(2) B. (1)(2)(3) C. (2)(3)(4) D. (4)(6)(1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=![]() 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).

(1)求k的值;
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
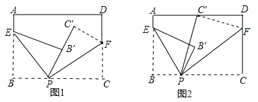
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y= ![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( ) 
A.b=2a+k
B.a=b+k
C.a>b>0
D.a>k>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( ) 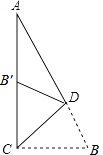
A.40°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) 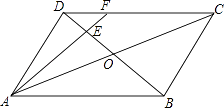
A.1:4
B.1:3
C.1:2
D.1:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
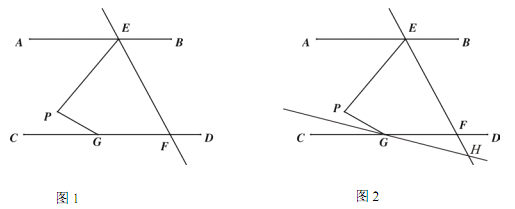
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com