
【题目】如图,点A在双曲线y= ![]() 上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( )
上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( ) 
A.8﹣2 ![]()
B.8+2 ![]()
C.3
D.6
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排![]() 人,问学校开设多少个“实践活动类”课程的班级比较合理?
人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解决问题:已知a=![]() ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:
∵a=![]() =
= =2﹣
=2﹣![]()
∴a﹣2=﹣![]()
∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简![]() +
+![]() +
+![]() +…+
+…+![]()
(2)若a=![]() ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在2×2的正方形网格中有9个格点,已经取定点A,B,C,在余下的6个点中任取一点P,满足△ABP与△ABC相似的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将n个边长都为2的正方形按如图所示摆放,点A1 , A2 , …An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( ) 
A.n
B.n﹣1
C.4(n﹣1)
D.4n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F.
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )

A. (1)(5)(2) B. (1)(2)(3) C. (2)(3)(4) D. (4)(6)(1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
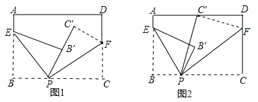
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com