
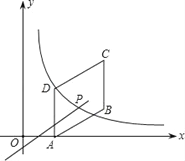
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)
【答案】(1)y=![]() ;(2)C(4,3);(3)见解析.
;(2)C(4,3);(3)见解析.
【解析】试题分析:(1)由B(4,1),C(4,3)得到BC⊥x轴,BC=2,根据平行四边形的性质得AD=BC=2,而A点坐标为(1,0),可得到点D的坐标为(1,2),然后把D(1,2)代入y=![]() 即可得到k=2,从而可确定反比例函数的解析式;
即可得到k=2,从而可确定反比例函数的解析式;
(2)把x=4代入y=mx+3﹣4m(m≠0)得到y=3,即可说明一次函数y=mx+3﹣4m(m≠0)的图象一定过点C;
(3)设点P的横坐标为x,由于一次函数y=mx+3﹣4m(m≠0)过C点,并且y随x的增大而增大时,则P点的纵坐标要小于3,横坐标要小于3,当纵坐标小于3时,由y=![]() 得到x>
得到x>![]() ,于是得到x的取值范围.
,于是得到x的取值范围.
试题解析:解:(1)∵B(4,1),C(4,3),
∴BC∥y轴,BC=2,
又∵四边形ABCD是平行四边形,
∴AD=BC=2,AD∥y轴,而A(1,0),
∴D(1,2),
∴由反比例函数y=![]() 的图象经过点D,可得k=1×2=2,
的图象经过点D,可得k=1×2=2,
∴反比例函数的解析式为y=![]() ;
;
(2)∵在一次函数y=mx+3﹣4m中,当x=4时,y=4m+3﹣4m=3,
∴一次函数y=mx+3﹣4m的图象一定过点C(4,3);
(3)点P的横坐标的取值范围:![]() <x<4.
<x<4.
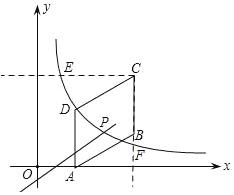
如图所示,过C(4,3)作y轴的垂线,交双曲线于E,作x轴的垂线,交双曲线于F,
当y=3时,3=![]() ,即x=
,即x=![]() ,
,
∴点E的横坐标为![]() ;
;
由点C的横坐标为4,可得F的横坐标为4;
∵一次函数y=mx+3﹣4m的图象一定过点C(4,3),且y随x的增大而增大,
∴直线y=mx+3﹣4m与双曲线的交点P落在EF之间的双曲线上,
∴点P的横坐标的取值范围是![]() <x<4.
<x<4.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )
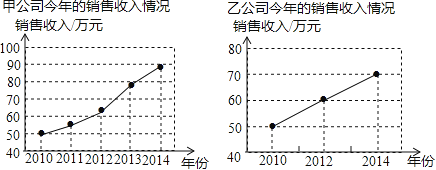
A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不一定正确的是 ( )
A..若 x y ,则 x c=y cB.若 x y ,则 xc yc
C.若 x y ,则![]() D.若
D.若![]() ,则 3x 2 y
,则 3x 2 y
查看答案和解析>>
科目:初中数学 来源: 题型:
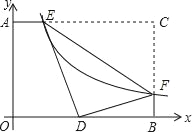
【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=![]() (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;
A | B | 合计(吨) | |
C |
| x | 240 |
D |
|
| 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(N>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
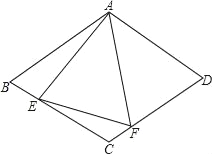
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
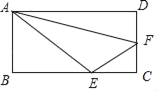
【题目】如图,点E、F分别在矩形ABCD的边BC和CD上,如果△ABE、△ECF、△FDA的面积分别刚好为6、2、5,那么矩形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com