练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

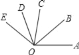
    【题目】如图，已知OB平分∠AOC，OD平分∠COE，∠AOD=110°，∠BOE=100°，求∠AOE的度数．

    【答案】140°

    【解析】

    设∠EOD=∠DOC=x°，求出∠AOB=∠COB=100°-2x°，根据∠AOD=110°得出方程，求出x的值，即可求出．

    解：∵OB平分∠AOC，OD平分∠COE，

    ∴设∠EOD=∠DOC=x°，∠AOB=∠COB，

    ∵∠AOD=110°，∠BOE=100°，

    ∴∠AOB=∠BOC=100°﹣2x°，

    ∴∠COD+∠COB+∠AOB=110°，

    ∴x+100﹣2x+100﹣2x=110，

    解得x=30，

    即∠EOD=∠DOC=30°，

    ∴∠AOE=∠AOD+∠DOE=110°+30°=140°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系 中，已知点 ， ．若平移点 到点 ，使以点 ， ， ， 为顶点的四边形是菱形，则正确的平移方法是（ ）

    A.向左平移1个单位，再向下平移1个单位
    B.向左平移 个单位，再向上平移1个单位
    C.向右平移 个单位，再向上平移1个单位
    D.向右平移1个单位，再向上平移1个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O是直线AB上一点，OC平分∠AOB，在直线AB另一侧，以O为顶点作∠DOE＝90°.

    (1)若∠AOE＝48°，则∠BOD＝______，∠AOE与∠BOD的关系是_______；

    (2)∠AOE与∠COD有什么关系？请写出你的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将6张小长方形纸片（如图1所示）按图2所示的方式不重叠的放在长方形ABCD内，未被覆盖的部分恰好分割为两个长方形，面积分别为S1和S2．已知小长方形纸片的长为a，宽为b，且a>b．当AB长度不变而BC变长时，将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内，S1与S2的差总保持不变，则a，b满足的关系是

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠．设顾客预计累计购物元()．

    (1)请用含的代数式分别表示顾客在两家超市购物所付的费用；

    (2)李明准备购买500元的商品，你认为他应该去哪家超市？请说明理由；

    (3)计算一下，李明购买多少元的商品时，到两家超市购物所付的费用一样？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD是⊙O的内接正方形，延长BA到E，使AE=AB，连接ED．

    （1）求证：直线ED是⊙O的切线；

    （2）连接EO交AD于点F，求证：EF=2FO．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形 的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，下列说法：

    ①a2+b2=13；②b2=1；③a2﹣b2=12；④ab=6．

    其中正确结论序号是________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙A，⊙B的半径分别为1cm，2cm，圆心距AB为5cm．如果⊙A由图示位置沿直线AB向右平移2cm，则此时该圆与⊙B的位置关系是（　　）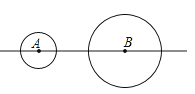

    A.外离
    B.相交
    C.外切
    D.内含

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．

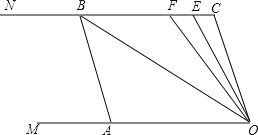
    （1）请在图中找出与∠AOC相等的角，并说明理由；

    （2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；

    （3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA度数；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案