
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
【答案】
(1)
证明:(1)连接OD.
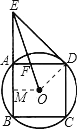
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)
证明:作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴ ![]()
∴EF=2FO.
【解析】(1)连接OD,只需证明OD⊥DE.根据正方形的性质得到AE=AD,则∠ADE=45°.又∠ADO=45°则证明了结论;(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.
【考点精析】认真审题,首先需要了解正多边形和圆(圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿CA往A运动,当运动到点A时停止.若设点D的运动时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,求CD、AD的长;
(2)在D运动过程中,△CBD能否为直角三角形,若不能,请说明理由,若能,请求出t的值;
(3)当t为何值时,△CBD是等腰三角形,请直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E是正方形ABCD的边CD外的一点,△DCE为等边三角形,BE交对角线AC于F .
(1)求∠AFD的度数;
(2)求证:AF = EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
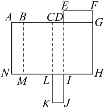
【题目】如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com