练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，有3张背面相同的纸牌A，B，C，其正面分别画有三个不同的几何图形，

    （1）求摸出一张纸片是中心对称图形的概率；

    （2）将这3张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．求摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的概率，（用树状图或列表法求解，纸牌可用A，B，C表示）

    【答案】（1）；（2）.

    【解析】

    （1）根据3张背面相同的纸牌A，B，C，只有2张纸片画着中心对称图形，即可求出得到中心对称图形的概率；（2）采用树状图或列表法求解，由于B（圆）与C（平行四边形）是中心对称图形，可得摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的有1种，继而利用概率公式即可求得答案．

    解：（1）∵3张牌中有2张牌是中心对称图形，

    ∴摸出一张纸片是中心对称图形的概率为．

    （2）画树状图如下：

    从树状图可以看出，所有可能出现的结果共有9个，这些结果出现的可能性相等，

    而摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的情况有1种，

    所以摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的概率为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图：公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处，他自己的影子恰好落在路灯CD的底部C处．晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在里程碑E处．

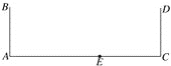
    (1)在图中画出杨老师的位置(用线段FG表示)，并画出光线，标明(太阳光、灯光)；

    (2)若上午上学时候高1米的木棒的影子为2米，杨老师身高为1.5米，他离里程碑E恰5米，求路灯高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：

    ①该产品90天售量（n件）与时间（第x天）满足一次函数关系，部分数据如下表：

    ②该产品90天内每天的销售价格与时间（第x天）的关系如下表：

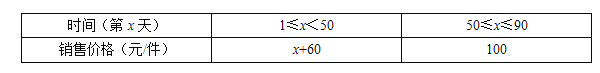
    （1）求出第10天日销售量；

    （2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品的销售利润最大？最大利润是多少？（提示：每天销售利润＝日销售量×（每件销售价格﹣每件成本））

    （3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知是关于x的二次函数.

    (1)求满足条件的k的值；

    (2)k为何值时，抛物线有最低点？求出这个最低点.当x为何值时，y的值随x值的增大而增大？

    (3)k为何值时，函数有最大值？最大值是多少？当x为何值时，y的值随x值的增大而减小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，E，F分别是DC和CB的延长线上的点，且DE＝BF，连接AE，AF，EF.

    (1)求证：△ADE≌△ABF；

    (2)填空：△ABF可以由△ADE绕旋转中心____点，按顺时针方向旋转___度得到；

    (3)若BC＝8，DE＝2，求△AEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

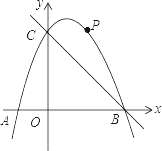
    【题目】如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．

    （1）求这个二次函数的表达式．

    （2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

    （3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时点P的坐标和四边形ABPC的最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°，此时该同学距地面高度AE为20米，电梯再上升5米到达D点，此时测得大楼BC楼顶B点的仰角为37°，求大楼的高度BC．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．

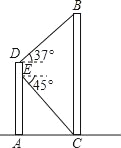
    查看答案和解析>>

    科目：初中数学 来源： 题型：

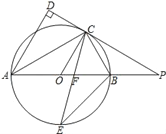
    【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB点F，连接BE．

    (1)求证：AC平分∠DAB；

    (2)求证：PC＝PF；

    (3)若tan∠ABC＝，AB＝14，求线段PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为迎接“全民阅读日“系列活动，某校围绕学生日人均阅读时间这一问题，对八年级学生进行随机抽样调查．如图是根据调查结果绘制成的统计图（不完整），请你根据图中提供的信息解答下列问题：

    （1）本次共抽查了八年级学生多少人；

    （2）请直接将条形统计图补充完整；

    （3）在扇形统计图中，11.5小时对应的圆心角是多少度；

    （4）根据本次抽样调查，估计全市50000名八年级学生日人均阅读时间状况，其中在0.51.5小时的有多少人？

    查看答案和解析>>

    同步练习册答案