
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНЉx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌAЕудкдЕуЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎЕуPЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЧвдкжБЯпBCЕФЩЯЗНЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиCOЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮ ABPCЕФУцЛ§зюДѓЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъКЭЫФБпаЮABPCЕФзюДѓУцЛ§ЃЎ
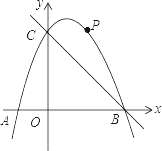
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ![]() ЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊ
ЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊ![]() ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉИљОнСтаЮЕФЖдНЧЯпЛЅЯрЦНЗжЃЌПЩЕУPЕуЕФзнзјБъЃЌИљОнКЏЪ§жЕгыздБфСПЕФЖдгІЙиЯЕЃЌПЩЕУД№АИЃЛЃЈ3ЃЉИљОнУцЛ§ЕФКЭВюЃЌПЩЕУЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУmЕФжЕЃЌИљОнздБфСПгыКЏЪ§жЕЕФЖдгІЙиЯЕЃЌПЩЕУPЕузјБъЃЎ
НтЃКЃЈ1ЃЉНЋBЁЂCСНЕуЕФзјБъДњШыЕУ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ
ЫљвдЖўДЮКЏЪ§ЕФБэДяЪНЮЊyЃНЉx2+2x+3ЃЛ
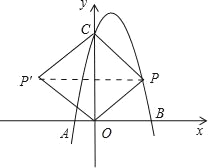
ЃЈ2ЃЉШчЭМЃЌ
 ЃЌ
ЃЌ
ДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃЎ
ЩшPЕузјБъЮЊЃЈxЃЌЉx2+2x+3ЃЉЃЌ
PPЁфНЛCOгкE
ШєЫФБпаЮPOPCЪЧСтаЮЃЌдђгаPCЃНPOЃЎ
СЌНгPPдђPEЁЭCOгкEЃЎ
ЁрOEЃНCEЃН![]() ЃЌ
ЃЌ
ЁрyЃН![]() ЃЎ
ЃЎ
ЁрЉx2+2x+3=![]() ЃЌ
ЃЌ
НтЕУx1ЃН![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЁрPЕуЕФзјБъЮЊ![]() ЃЎ
ЃЎ
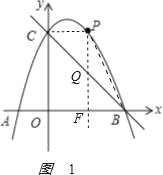
ЃЈ3ЃЉШчЭМ1ЃЌ
 ЃЌ
ЃЌ
Й§ЕуPзїyжсЕФЦНааЯпгыBCНЛгкЕуQЃЌгыOBНЛгкЕуFЃЌЩшPЃЈxЃЌЉx2+2x+3ЃЉ
взЕУЃЌжБЯпBCЕФНтЮіЪНЮЊyЃНЉx+3ЃЎ
дђQЕуЕФзјБъЮЊЃЈxЃЌЉx+3ЃЉЃЎ
PQЃНЉx2+3xЃЎ
SЫФБпаЮABPCЃНSЁїABC+SЁїBPQ+SЁїCPQЃН![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF
QPOF
ЃН![]() ЁС4ЁС3+
ЁС4ЁС3+![]() ЃЈЉx2+3xЃЉЁС3
ЃЈЉx2+3xЃЉЁС3
ЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЕБx=![]() ЪБЃЌЫФБпаЮABPCЕФУцЛ§зюДѓ
ЪБЃЌЫФБпаЮABPCЕФУцЛ§зюДѓ
ДЫЪБPЕуЕФзјБъЮЊ![]() ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ


 ЬНОПгыЙЎЙЬКгФЯПЦбЇММЪѕГіАцЩчЯЕСаД№АИ
ЬНОПгыЙЎЙЬКгФЯПЦбЇММЪѕГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГЙЄМўЕФЖўЪгЭМЃЌАДЭМжаГпДчЧѓЙЄМўЕФБэУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃН6cmЃЌBCЃН12cmЃЌЁЯBЃН90ЁуЃЎЕуPДгЕуAПЊЪМбиABБпЯђЕуBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуBПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЌШчЙћP,QЗжБ№ДгA,BЭЌЪБГіЗЂЃЌЩшвЦЖЏЪБМфЮЊtЃЈsЃЉЃЎ

ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЁїPBQЕФУцЛ§ЃЛ
ЪБЃЌЧѓЁїPBQЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊЖрЩйЪБЃЌЫФБпаЮAPQCЕФУцЛ§зюаЁЃПзюаЁУцЛ§ЪЧЖрЩйЃП
ЮЊЖрЩйЪБЃЌЫФБпаЮAPQCЕФУцЛ§зюаЁЃПзюаЁУцЛ§ЪЧЖрЩйЃП
ЃЈ3ЃЉЕБ![]() ЮЊЖрЩйЪБЃЌЁїPQBгыЁїABCЯрЫЦЃЎ
ЮЊЖрЩйЪБЃЌЁїPQBгыЁїABCЯрЫЦЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
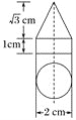
ЁОЬтФПЁПШчЭМЫљЪОЃЌМзЮяЬхИп4УзЃЌгАГЄ3УзЃЌввЮяЬхИп2УзЃЌгАГЄ4УзЃЌСНЮяЬхЯрОр5УзЃЎ
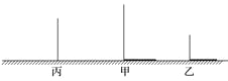
(1)дкЭМжаЛГіЕЦЕФЮЛжУЃЌВЂЛГіБћЮяЬхЕФгАзгЃЎ
(2)ШєЕЦИЫЃЌМзЁЂввЖМгыЕиУцДЙжБВЂЧвдкЭЌвЛжБЯпЩЯЃЌЪдЧѓГіЕЦЕФИпЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌга3еХБГУцЯрЭЌЕФжНХЦAЃЌBЃЌCЃЌЦфе§УцЗжБ№ЛгаШ§ИіВЛЭЌЕФМИКЮЭМаЮЃЌ

ЃЈ1ЃЉЧѓУўГівЛеХжНЦЌЪЧжааФЖдГЦЭМаЮЕФИХТЪЃЛ
ЃЈ2ЃЉНЋет3еХжНХЦБГУцГЏЩЯЯДдШКѓУўГівЛеХЃЌЗХЛиЯДдШКѓдйУўГівЛеХЃЎЧѓУўГіСНеХХЦУцЭМаЮМШЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЕФжНХЦЕФИХТЪЃЌЃЈгУЪїзДЭМЛђСаБэЗЈЧѓНтЃЌжНХЦПЩгУAЃЌBЃЌCБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧ![]() ЕФжБОЖЃЌЕуCЁЂDдк
ЕФжБОЖЃЌЕуCЁЂDдк![]() ЩЯЃЌЧвADЦНЗж
ЩЯЃЌЧвADЦНЗж![]() ЃЌЙ§ЕуDзїACЕФДЙЯпЃЌгыACЕФбгГЄЯпЯрНЛгкEЃЌгыABЕФбгГЄЯпЯрНЛгкЕуFЃЌGЮЊABЕФЯТАыдВЛЁЕФжаЕуЃЌDGНЛABгкHЃЌСЌНгDBЁЂGBЃЎ
ЃЌЙ§ЕуDзїACЕФДЙЯпЃЌгыACЕФбгГЄЯпЯрНЛгкEЃЌгыABЕФбгГЄЯпЯрНЛгкЕуFЃЌGЮЊABЕФЯТАыдВЛЁЕФжаЕуЃЌDGНЛABгкHЃЌСЌНгDBЁЂGBЃЎ
![]() жЄУїEFЪЧ
жЄУїEFЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
![]() ЧѓжЄЃК
ЧѓжЄЃК![]() ЃЛ
ЃЛ
![]() вбжЊдВЕФАыОЖ
вбжЊдВЕФАыОЖ![]() ЃЌ
ЃЌ![]() ЃЌЧѓGHЕФГЄЃЎ
ЃЌЧѓGHЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
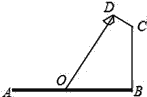
ЁОЬтФПЁПШчЭМЃЌвЊдкПэABЮЊ20УзЕФъБКЃДѓЕРСНБпАВзАТЗЕЦЃЌТЗЕЦЕФЕЦБлCDгыЕЦжљBCГЩ120ЁуНЧЃЌЕЦежЕФжсЯпDOгыЕЦБлCDДЙжБЃЌЕБЕЦежЕФжсЯпDOЭЈЙ§ЙЋТЗТЗУцЕФжааФЯпЃЈМДOЮЊABЕФжаЕуЃЉЪБееУїаЇЙћзюМбЃЌШєCD=![]() УзЃЌдђТЗЕЦЕФЕЦжљBCИпЖШгІИУЩшМЦЮЊ____УзЃЈМЦЫуНсЙћБЃСєИљКХЃЉЃЎ
УзЃЌдђТЗЕЦЕФЕЦжљBCИпЖШгІИУЩшМЦЮЊ____УзЃЈМЦЫуНсЙћБЃСєИљКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
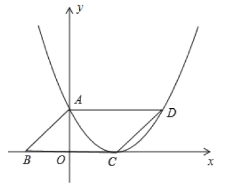
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮжаЃЌБпBCдкxжсЩЯ.ЧвBC=6ЃЌЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ12ЃЌCЪЧХзЮяЯпЖЅЕуЃЌAЃЌDдкХзЮяЯпЩЯЃЌЧѓХзЮяЯпЕФНтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп yЃНax2Љ5ax+c НЛ x жсгкЕу AЃЌЕу A ЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
(1)гУКЌ a ЕФДњЪ§ЪНБэЪО cЃЎ
(2)ЕБ aЃН![]() ЪБЃЌЧѓ x ЮЊКЮжЕЪБ y ШЁЕУзюаЁжЕЃЌВЂЧѓГі y ЕФзюаЁжЕЃЎ
ЪБЃЌЧѓ x ЮЊКЮжЕЪБ y ШЁЕУзюаЁжЕЃЌВЂЧѓГі y ЕФзюаЁжЕЃЎ
(3)ЕБ aЃН![]() ЪБЃЌЧѓ 0ЁмxЁм6 ЪБ y ЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧѓ 0ЁмxЁм6 ЪБ y ЕФШЁжЕЗЖЮЇЃЎ
(4)вбжЊЕу B ЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌЕБХзЮяЯпЕФЖЅЕуТфдкЁїAOB ЭтНгдВФкВПЪБЃЌжБНгаДГі aЕФШЁжЕЗЖЮЇЃЎ
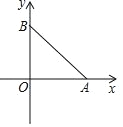
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com