练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

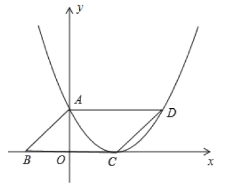
    【题目】如图，在平行四边形中，边BC在x轴上.且BC=6，平行四边形ABCD的面积为12，C是抛物线顶点，A，D在抛物线上，求抛物线的解析式.

    【答案】y=（x-3）2

    【解析】

    由平行四边形ABCD的面积为12且BC=6易得A（0，2），再由抛物线的对称性及AD=BC=6易得抛物线的对称轴为直线x=3，则可知顶点C的坐标为（3，0）；设顶点式，代入A点即可求解抛物线解析式.

    平行四边形ABCD的面积为12，

    ∵.，

    ∴，

    ∴A（0，2），

    ∵四边形ABCD为平行四边形，

    ∴AD=BC=6，AD//BC，

    ∴A、D为抛物线上的对称点，

    ∴抛物线的对称轴为直线x=3，

    ∴顶点C的坐标为（3，0），

    设抛物线的解析式为，把A（0，2）代入，

    得，解得a=，

    ∴抛物线的解析式为y=（x-3）2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下列一组方程：；；；；它们的根有一定的规律，都是两个连续的自然数，我们称这类一元二次方程为“连根一元二次方程”．

    若也是“连根一元二次方程”，写出k的值，并解这个一元二次方程；

    请写出第n个方程和它的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

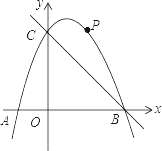
    【题目】如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．

    （1）求这个二次函数的表达式．

    （2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

    （3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时点P的坐标和四边形ABPC的最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

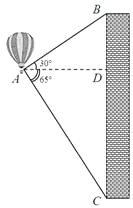
    【题目】（6分）如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120m．求这栋高楼的高度．（结果用含非特殊角的三角函数及根式表示即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

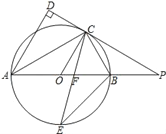
    【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB点F，连接BE．

    (1)求证：AC平分∠DAB；

    (2)求证：PC＝PF；

    (3)若tan∠ABC＝，AB＝14，求线段PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．

    （1）求抛物线及直线AC的函数关系式；

    （2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；

    （3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

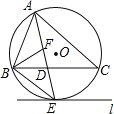
    【题目】如图，圆O是的外接圆，AE平分交圆O于点E，交BC于点D，过点E作直线．

    （1）判断直线l与圆O的关系，并说明理由；

    （2）若的平分线BF交AD于点F，求证：；

    （3）在（2）的条件下，若，，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

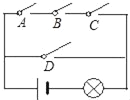
    【题目】如图．电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光．

    (1)任意闭合其中一个开关，则小灯泡发光的概率等于　 　；

    (2)任意闭合其中两个开关，请用画树状图或列表的方法求出小灯泡发光的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题探究

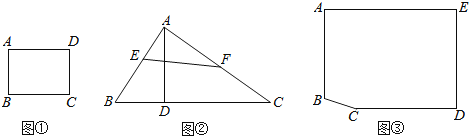
    （1）如图①，在矩形ABCD中，AB=3，BC=4，如果BC边上存在点P，使△APD为等腰三角形，那么请画出满足条件的一个等腰三角形△APD，并求出此时BP的长；

    （2）如图②，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点，当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长；

    问题解决

    （3）有一山庄，它的平面图为如图③的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安装监控装置，用来监视边AB，现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳，已知∠A=∠E=∠D=90°，AB=270m，AE=400m，ED=285m，CD=340m，问在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案