
【题目】已知![]() 是关于x的二次函数.
是关于x的二次函数.
(1)求满足条件的k的值;
(2)k为何值时,抛物线有最低点?求出这个最低点.当x为何值时,y的值随x值的增大而增大?
(3)k为何值时,函数有最大值?最大值是多少?当x为何值时,y的值随x值的增大而减小?
【答案】(1)k=±2;(2) 见解析;(3)见解析.
【解析】
(1)直接利用二次函数定义得出符合题意的k的值;
(2)抛物线有最低点,所以开口向上,k+1大于0,再根据(1)中k的值即可确定满足条件的值,再根据二次函数性质,即可得最低点的坐标和函数的单调区间;
(3)函数有最大值,可得抛物线的开口向下,k+1小于0,再根据(1)中k的值即可确定满足条件的值,然后根据二次函数性质可求得最大值和函数单调区间.
(1) 根据二次函数的定义得 ![]() 解得k=±2.
解得k=±2.
∴当k=±2时,原函数是二次函数.
(2) 根据抛物线有最低点,可得抛物线的开口向上,
∴k+1>0,即k>-1,根据第(1)问得:k=2.
∴该抛物线的解析式为![]() ,∴抛物线的顶点为(0,0),当x>0时,y随x的增大而增大.
,∴抛物线的顶点为(0,0),当x>0时,y随x的增大而增大.
(3) 根据二次函数有最大值,可得抛物线的开口向下,
∴k+1<0,即k<-1,根据第(1)问得:k=-2.
∴该抛物线的解析式为![]() ,顶点坐标为(0,0),
,顶点坐标为(0,0),
∴当k=-2时,函数有最大值为0. 当x>0时,y随x的增大而减小.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
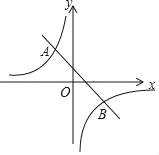
【题目】如图,已知A(m,2),B(2,n)是一次函数y=﹣x+1的图象与反比例函数y=![]() (k≠0)图象的两个交点.
(k≠0)图象的两个交点.
(1)求反比例函数的解析式;
(2)根据图象,请直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).

(1)当![]() 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,该商品的进价为每件80元,现在的售价为每件145元,每天可销售40件![]() 商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件
商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件![]() 若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
![]() Ⅰ
Ⅰ![]() 用含x的式子表示:
用含x的式子表示:
![]() 每件商品的售价为______元;
每件商品的售价为______元;
![]() 每天的销售量为______件;
每天的销售量为______件;
![]() Ⅱ
Ⅱ![]() 求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
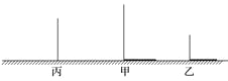
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形,

(1)求摸出一张纸片是中心对称图形的概率;
(2)将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.求摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的概率,(用树状图或列表法求解,纸牌可用A,B,C表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
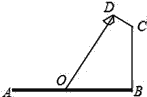
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处与灯塔P的距离约为_______nmile.(结果取整数,参考数据:![]() =1.7,
=1.7, ![]() ≈ 1.4)
≈ 1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com